- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:22.
- Última modificação 2025-01-23 12:43.
Dividir uma fração por uma fração pode parecer confuso no início, mas na verdade é muito fácil. Tudo que você precisa fazer é inverter, multiplicar e simplificar! Este artigo o guiará pelo processo e mostrará como é fácil dividir uma fração por uma fração.
Etapa
Parte 1 de 2: Noções básicas sobre como dividir frações por frações
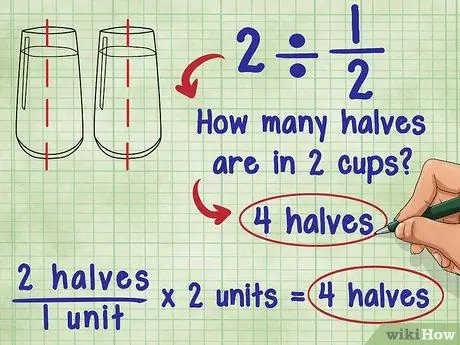
Etapa 1. Pense no que significa dividir por uma fração
Cerca de 2 ÷ 1/2 perguntou Ada: "Quantas metades estão em 2?" A resposta é 4 porque cada unidade (1) consiste em duas “metade”, e há 2 unidades no total: 2 “metade” / 1 unidade * 2 unidades = 4 “metade”.
- Tente imaginar a mesma equação usando um copo de água: quantos copos e meio de água existem em 2 copos de água? Você pode colocar 2 xícaras e meio de água em cada copo de água. Isso significa que, basicamente, você soma os “meio” copos de água e tem dois copos: 2 “meio” / 1 xícara * 2 xícaras = 4 “meio”.
- Isso significa que se a fração que você está dividindo estiver entre 0 e 1, a resposta será sempre maior que o número original! Isso é verdade quando você divide um número inteiro ou fração por uma fração.

Etapa 2. Compreenda que dividir é o oposto de multiplicar
Assim, a divisão por uma fração pode ser resolvida multiplicando pelo recíproco da fração. O recíproco de uma fração (também chamado de “multiplicação inversa”) é a fração que é invertida, de modo que o numerador e o denominador trocam de lugar. Em um momento, estaremos dividindo frações por frações, encontrando o recíproco da segunda fração e multiplicando ambas as frações. No entanto, vamos examinar alguns dos opostos primeiro:
- O recíproco de 3/4 é 4/3.
- O oposto de 7/5 é 5/7.
- O recíproco de 1/2 é 2/1 ou 2.
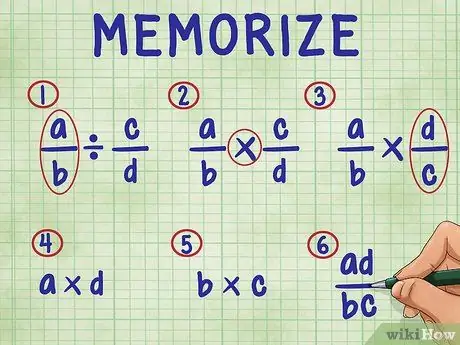
Etapa 3. Lembre-se das etapas a seguir para dividir uma fração por uma fração
Em ordem, as etapas incluem:
- Basta deixar a primeira fração da equação.
- Mude o sinal de divisão para o sinal de multiplicação.
- Inverta a segunda fração (encontre seu recíproco).
- Multiplique o numerador (número superior) de ambas as frações. O resultado da multiplicação é o numerador (topo) da sua resposta.
- Multiplique o denominador (número inferior) de ambas as frações. O produto do produto é o denominador de sua resposta.
- Simplifique suas frações, simplificando-as em seus termos mais simples.
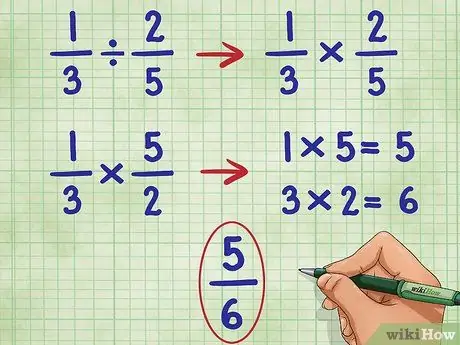
Etapa 4. Execute essas etapas para o exemplo 1/3 2/5
Começaremos deixando de fora a primeira fração e convertendo o sinal de divisão para o sinal de multiplicação:
- 1/3 ÷ 2/5 = Torna-se:
- 1/3 * _ =
- Agora, invertemos a segunda fração (2/5) para encontrar seu recíproco, que é 5/2:
- 1/3 * 5/2 =
- Agora, multiplique o numerador (número superior) de ambas as frações, 1 * 5 = 5.
- 1/3 * 5/2 = 5/
- Agora, multiplique o denominador (número inferior) de ambas as frações, 3 * 2 = 6.
- Agora, temos: 1/3 * 5/2 = 5/6
- Esta fração não pode ser simplificada mais, então temos nossa resposta.

Etapa 5. Tente se lembrar das seguintes rimas para ajudá-lo a se lembrar:
"Dividir as frações é fácil, inverta a segunda fração e depois multiplique. Não se esqueça de simplificar, antes da hora de comer."
Outro lembrete de ajuda útil informa o que fazer com cada parte da equação: “Deixe-me (primeira fração), Mudar-me (sinal de divisão), Inverter-me (segunda fração).”
Parte 2 de 2: Dividindo Frações por Frações em Problemas
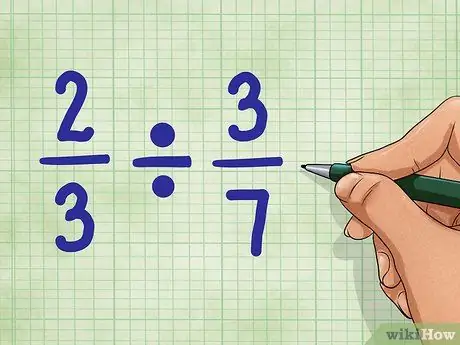
Etapa 1. Comece com exemplos de perguntas
Vamos usar 2/3 ÷ 3/7. Esta questão pede o número de peças igual a 3/7, que pode ser encontrado no valor 2/3. Não se preocupe. Não é tão difícil quanto parece!
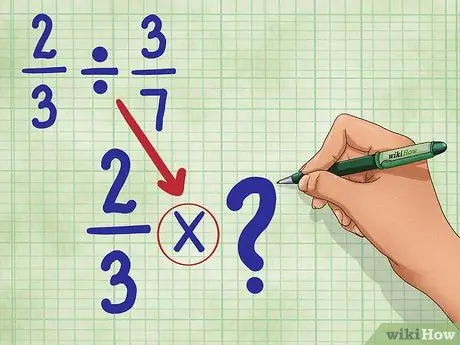
Etapa 2. Converta o sinal de divisão para o sinal de multiplicação
Sua nova equação será: 2/3 * _ (Estaremos preenchendo este espaço em um momento.)
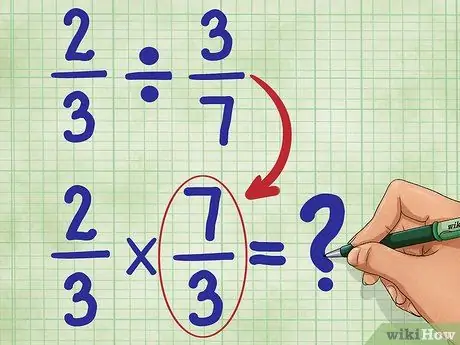
Etapa 3. Agora, encontre o recíproco da segunda fração
Isso significa inverter 3/7 para que o numerador (3) esteja agora na parte inferior e o denominador (7) no topo. O recíproco de 3/7 é 7/3. Agora, escreva sua nova equação:
2/3 * 7/3 = _

Etapa 4. Multiplique suas frações
Primeiro, multiplique os numeradores de ambas as frações: 2 * 7 = 14. 14 é o numerador (número superior) de sua resposta. Em seguida, multiplique os denominadores de ambas as frações: 3 * 3 = 9. 9 é o denominador (número inferior) de sua resposta. Agora você sabe disso 2/3 * 7/3 = 14/9.
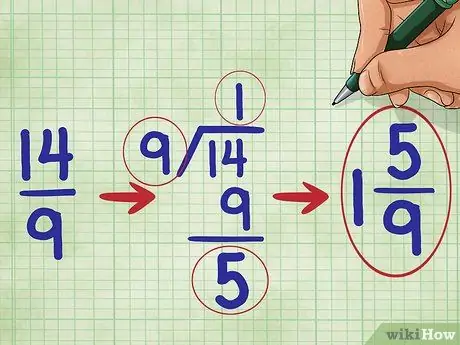
Etapa 5. Simplifique sua fração
Nesse problema, como o numerador da fração é maior que o denominador, sabemos que nossa fração é maior que 1. Devemos convertê-la em um número misto. (Um número misto é um número inteiro e uma fração combinados, por exemplo 1 2/3.))
-
Primeiro, divida o numerador
Etapa 14. com 9.
O número 14 dividido por 9 é igual a um com o resto de 5, então você deve escrever sua fração simplificada como: 1 5/9 (“Um cinco nove”).
- Pare, você encontrou a resposta! Você pode especificar que não pode mais simplificar a fração porque o denominador não é divisível pelo numerador (9 não é divisível por 5) e o numerador é um número primo, ou um inteiro que só é divisível por um e o próprio número.
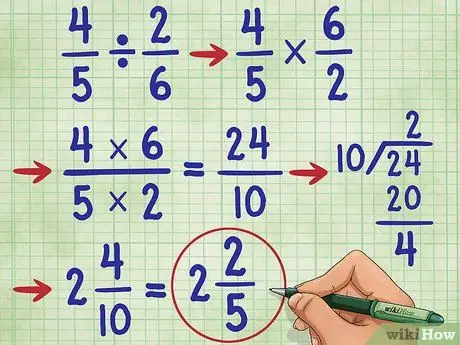
Etapa 6. Experimente outro exemplo
Vamos tentar a pergunta 4/5 ÷ 2/6 =. Primeiro, mude o sinal de divisão para o sinal de multiplicação (4/5 * _ =) e, em seguida, encontre o recíproco de 2/6, que é 6/2. Agora, você tem a equação: 4/5 * 6/2 =_. Agora, multiplique o numerador, 4 * 6 = 24, e o denominador 5* 2 = 10. Agora você tem 4/5 * 6/2 = 24/10.
Agora, simplifique a fração. Como o numerador é maior que o denominador, devemos converter essa fração em um número misto.
- Primeiro, divida o numerador pelo denominador, (24/10 = 2 restantes 4).
- Escreva a resposta como 2 4/10. Ainda podemos simplificar essa fração novamente!
- Observe que 4 e 10 são números pares. Portanto, o primeiro passo para simplificar é dividir cada número por 2. Obtemos 2/5.
- Como o denominador (5) não é divisível pelo numerador (2) e 5 é um número primo, sabemos que essa fração não pode ser mais simplificada. Então, nossa resposta é: 2 2/5.

Etapa 7. Obtenha ajuda adicional para simplificar as frações
Você provavelmente gastou muito tempo aprendendo como simplificar as frações antes de tentar dividi-las. No entanto, se você precisar de uma atualização ou de alguma outra ajuda, existem alguns ótimos artigos online que podem ser de grande ajuda para você.
Artigos relacionados ao wikiHow
- Conversão de frações comuns em decimais
- Calculando a área de um círculo
- Dividindo Polinômios Usando Divisão Sintética
- Divisão de frações mistas






