Dividir frações por números inteiros não é tão difícil quanto parece. Para dividir uma fração por um inteiro, tudo o que você precisa fazer é converter o número inteiro em uma fração, encontrar o recíproco da fração e multiplicar o resultado pela primeira fração. Se você quiser saber como fazer, basta seguir estas etapas:
Etapa
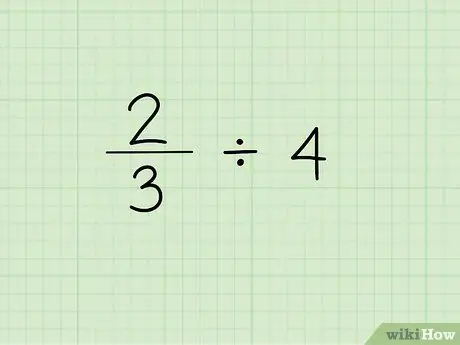
Etapa 1. Anote o problema
O primeiro passo para dividir uma fração por um inteiro é escrever a fração seguida pelo sinal de divisão e o inteiro que você precisa para dividir a fração. Digamos que estejamos trabalhando com o seguinte problema: 2/3 4.
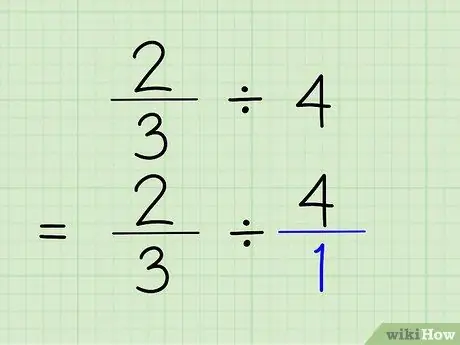
Etapa 2. Converta inteiros em frações
Para converter um inteiro em uma fração, tudo o que você precisa fazer é colocar o inteiro acima do número 1. O inteiro se torna o numerador e 1 se torna o denominador da fração. Dizer 4/1 é realmente o mesmo que dizer 4, porque você só está mostrando que o número contém "1" 4 vezes. O problema será 2/3 4/1.
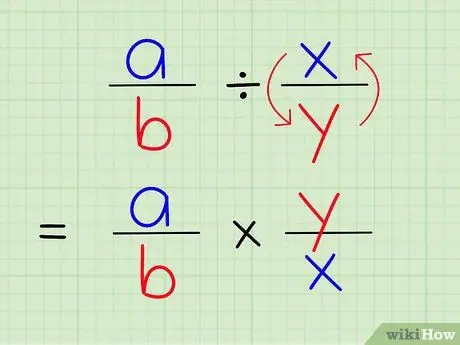
Etapa 3. Dividir uma fração por outra é o mesmo que multiplicar essa fração pelo recíproco de outra fração
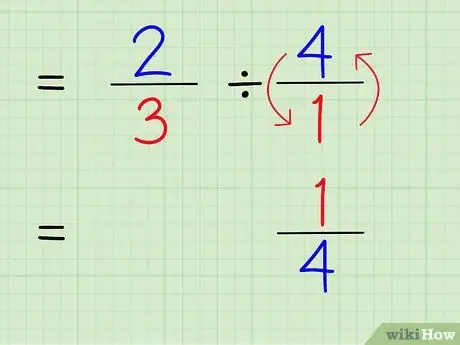
Etapa 4. Escreva o recíproco do inteiro
Para encontrar o inverso de um número, troque o numerador e o denominador do número. Portanto, para encontrar o recíproco de 4/1, basta trocar o numerador e o denominador para que o número se torne 1/4.
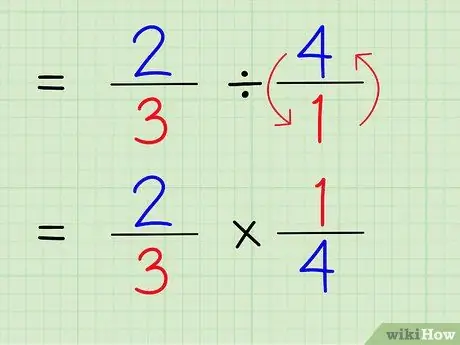
Etapa 5. Mude o sinal de divisão para o sinal de multiplicação
O problema será 2/3 x 1/4.
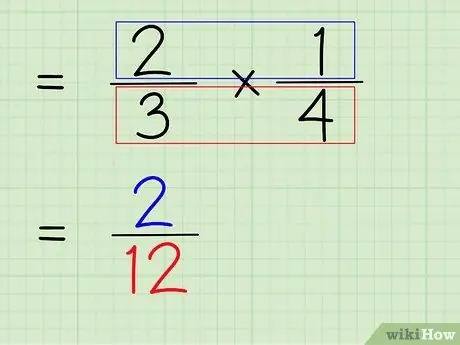
Etapa 6. Multiplique o numerador e o denominador da fração
Portanto, a próxima etapa é multiplicar o numerador e o denominador da fração para obter um novo numerador e denominador como a resposta final.
- Para multiplicar os numeradores, basta multiplicar 2 x 1 para obter 2.
- Para multiplicar os denominadores, basta multiplicar 3 x 4 para obter 12.
- 2/3 x 1/4 = 2/12
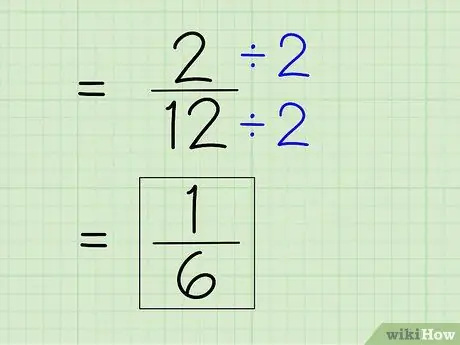
Etapa 7. Simplifique a fração
Para simplificar uma fração, você deve encontrar o menor denominador, o que significa que você deve dividir o numerador e o denominador por qualquer número que divida ambos os números. Como 2 é o numerador, você terá que ver se 2 pode dividir 12 completamente - pode porque 12 é um número par. Em seguida, divida o numerador e denominador por 2 para obter um novo numerador e denominador para obter uma resposta simples.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- A fração 2/12 pode ser simplificada para 1/6. Esta é sua resposta final.
Pontas
- Isso serve para auxiliar a memória, uma maneira fácil de lembrar como fazer todos esses cálculos. Lembre-se: "É fácil dividir frações, inverter o segundo número e multiplicar!"
- Outra variação do método acima é JGB / JBG. Não mude o primeiro número. Mude para multiplicação. Inverta o último número. Ou B primeiro, depois G.
- Se você cancelar o cálculo antes de multiplicá-lo, pode não precisar encontrar a forma mais simples da fração porque o resultado já está na forma de fração mais simples, como você pode ver. Em nosso exemplo, antes de multiplicarmos 2/3 × 1/4, podemos ver que o primeiro numerador (2) e o segundo denominador (4) têm o mesmo multiplicador de 2, que podemos cancelar antes de continuar o cálculo. Isso converte o problema para 1/3 × 1/2, o que dá um resultado 1/6 imediato e nos economiza tempo ao simplificar a fração em um estágio posterior.
- Se uma de suas frações for negativa, esse método ainda é viável; certifique-se de acompanhar os sinais ao realizar essas etapas.
