É fácil multiplicar frações por números mistos ou números inteiros. Comece convertendo frações mistas ou números inteiros em frações impróprias (frações com um numerador maior que o denominador). Multiplique o numerador das duas frações. Depois disso, multiplique os dois denominadores e simplifique o produto.
Etapa
Método 1 de 2: Multiplicando duas frações mistas
Etapa 1. Converta frações mistas em frações impróprias
Para converter um número misto, multiplique o denominador por um número inteiro existente. Depois disso, adicione um numerador ao produto. Coloque o resultado final acima da linha e não altere o denominador. Repita esta etapa para as outras frações mistas.
Por exemplo, se você tiver um problema de multiplicação de 1 1/2 x 4 4/7, converta ambas as frações em frações impróprias. A fração 1 1/2 pode ser alterada para 3/2 e 4 4/7 é alterada para 32/7. Agora, seu problema de multiplicação torna-se 3/2 x 32/7
Etapa 2. Multiplique o numerador de ambas as frações
Quando você tiver duas frações impróprias e nenhum número inteiro no problema, multiplique os dois numeradores. Escreva o resultado e coloque-o acima da linha.
- O numerador está sempre no topo da fração.
- Por exemplo, para o problema 3/2 x 32/7, multiplique 3 por 32 para obter 96.
Etapa 3. Multiplique os denominadores de ambas as frações
Agora multiplique o número sob a linha e escreva o resultado sob o numerador.
Por exemplo, para o problema 3/2 x 32/7, multiplique 2 por 7 para obter 14
Etapa 4. Converta as respostas em frações mistas, se possível
Se o numerador do produto for maior que o denominador, encontre um número que produza um número que se aproxime do numerador quando multiplicado pelo denominador (este número atuará como um inteiro posteriormente). Depois disso, coloque a diferença entre o produto do denominador pelo número inteiro e o numerador sobre o denominador para obter a forma de número misto.
- Por exemplo, se você obtiver 96/14 como resultado da multiplicação, encontre o número que resulta em uma soma próxima a 96 quando multiplicado por 14. Esse número é 6 e você obtém 12 como a diferença entre 14 x 6 e 96. Coloque 12 acima do denominador (14).
- Normalmente, o professor pedirá que você escreva a resposta da mesma forma que a pergunta. Se você obtiver um número misto como um problema, também precisará converter a resposta em um número misto.
Etapa 5. Simplifique ainda mais os resultados, se possível
É possível que você obtenha números inteiros e frações. Observe as frações e verifique se podem ser simplificadas. Por exemplo, se você tiver um resultado de 6 12/14, divida 12/14 por 2 para simplificar para 6/7.
Neste exemplo de problema, sua resposta final seria 6 6/7
Método 2 de 2: multiplique as frações por inteiros
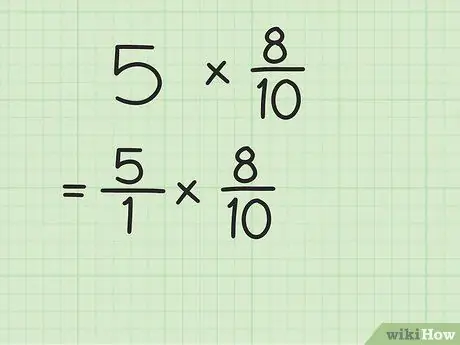
Etapa 1. Reescreva o número inteiro como uma fração
Para reescrever um inteiro como uma fração, simplesmente coloque-o acima do número 1 (o denominador). Depois disso, os inteiros existentes se transformarão em frações impróprias.
Por exemplo, se você tiver um problema de 5 x 8/10, coloque 5 acima do número 1. Agora a multiplicação é 5/1 x 8/10
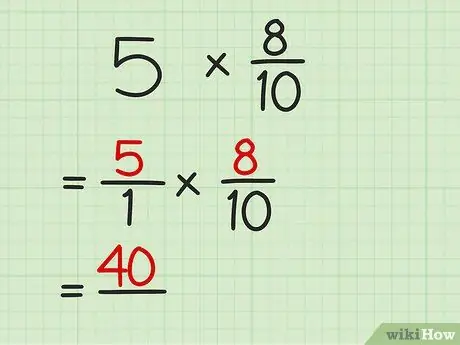
Etapa 2. Multiplique o numerador de ambas as frações
Lembre-se de que o numerador é o número que está acima da linha. Anote o resultado e coloque uma linha sob o produto.
Por exemplo, no problema 5/1 x 8/10, multiplique 5 por 8 para obter 40
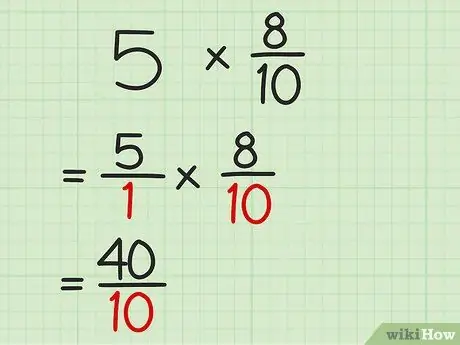
Etapa 3. Multiplique os denominadores de ambas as frações
Neste ponto, você pode multiplicar os números abaixo da linha para obter o denominador do produto. Agora você tem uma resposta de multiplicação em forma de fração.
Por exemplo, para um problema 5/1 x 8/10, multiplique 1 por 10 para obter 10. Coloque o número sob a linha de forma que o produto das duas frações seja 40/10
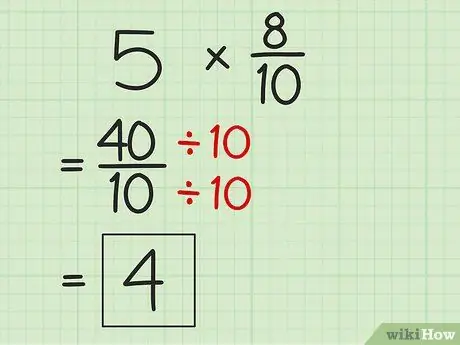
Etapa 4. Recolha as respostas, se possível
Uma vez que o produto do produto pode ser uma fração imprópria, simplifique o resultado para a menor forma. Divida o numerador pelo denominador para obter um resultado mais simples.
- Para simplificar 40/10, divida 40 por 10 para obter 4 como a nova resposta para o problema de multiplicação.
- Normalmente, você obtém números mistos porque o resultado da divisão terá um resto.
