- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:15.
- Última modificação 2025-01-23 12:43.
Qualquer pessoa pode aprender matemática, quer já esteja em um estágio superior na escola ou apenas queira aprimorar o básico novamente. Depois de discutir como ser um bom aluno em matemática, este artigo ensinará as progressões matemáticas básicas e os elementos básicos que você precisará aprender em cada prática. Em seguida, este artigo discutirá os fundamentos do aprendizado de aritmética, o que ajudará tanto crianças do ensino fundamental quanto todos que desejam aprender os fundamentos dessa área da ciência.
Etapa
Parte 1 de 6: segredos para se tornar um bom aluno de matemática

Etapa 1. Aparecer na aula
Quando você faltar à aula, você deve aprender conceitos com colegas de classe ou com seu livro didático. Você nunca receberá um resumo em texto de um amigo tanto quanto recebe de seu professor.
- Chegue para aula na hora certa. Em vez disso, chegue um pouco mais cedo e abra seu caderno no lugar certo, abra seu livro e tire sua calculadora para estar pronto para começar quando seu professor estiver pronto para ensinar.
- Falta apenas se estiver doente. Se você realmente perder a aula, peça a seus colegas para descobrirem sobre o que o professor estava falando e que lição de casa foi dada.

Etapa 2. Trabalhe com seu professor
Se o seu professor está trabalhando em um problema na frente da classe, trabalhe com o professor trabalhando no problema em seu caderno.
- Certifique-se de que suas notas sejam claras e fáceis de ler. Não escreva apenas perguntas. Anote também qualquer coisa que o professor disser que possa melhorar sua compreensão dos conceitos explicados.
- Responda às perguntas de exemplo fornecidas por seu professor. Conforme o professor percorre a classe enquanto você trabalha, responda às perguntas que forem feitas.
- Participe quando o professor resolver um problema. Não espere que o professor ligue para você. Ofereça-se para responder quando souber a resposta e levante a mão para fazer uma pergunta se não tiver certeza do material que está sendo ensinado.

Etapa 3. Faça a lição de casa no mesmo dia em que for entregue
Se você fizer sua lição de casa no mesmo dia, o conceito ainda está fresco em sua mente. Às vezes, não é possível terminar sua lição de casa no mesmo dia. Certifique-se de que sua lição de casa seja feita antes de ir para a aula.

Etapa 4. Trabalhe fora da classe se precisar de ajuda
Visite seu professor durante os intervalos ou durante o horário de expediente.
- Se você tem um Centro de Matemática em sua escola, descubra o horário de funcionamento e peça ajuda.
- Junte-se a um grupo de estudo. Um bom grupo de estudo geralmente consiste de 4 ou 5 pessoas com diferentes níveis de habilidade. Se você é um aluno "C" em matemática, junte-se a um grupo de 2 ou 3 alunos com notas "A" ou "B" para que possa melhorar suas habilidades. Evite ingressar em um grupo de alunos com notas inferiores às suas.
Parte 2 de 6: Aprendendo matemática na escola

Etapa 1. Comece com aritmética
Na maioria das escolas, os alunos aprendem aritmética no ensino fundamental. A aritmética abrange os conceitos básicos de adição, subtração, multiplicação e divisão.
- Faça perguntas práticas. Resolver problemas aritméticos repetidamente é a melhor maneira de memorizar o básico corretamente. Procure um software que possa fornecer uma ampla variedade de problemas matemáticos diferentes para trabalhar. Além disso, procure problemas com prazos para melhorar sua velocidade.
- Você também pode encontrar problemas aritméticos online e pode baixar aplicativos aritméticos para o seu dispositivo móvel.

Etapa 2. Continue com a pré-álgebra
Este exercício fornecerá os elementos básicos de que você precisará para resolver problemas de álgebra posteriormente.
- Saiba mais sobre frações e decimais. Você aprenderá a somar, subtrair, multiplicar e dividir frações e decimais. Com relação às frações, você aprenderá como subtrair frações e traduzir números combinados. Com relação aos decimais, você entenderá os valores de posição e será capaz de usar decimais em problemas de história.
- Aprenda sobre proporções, proporções e porcentagens. Esses conceitos o ajudarão a aprender a fazer comparações.
- Apresente-se à geometria básica. Você aprenderá formas e conceitos 3D. Você também aprenderá conceitos como área, perímetro, volume e área de superfície, bem como informações sobre linhas e ângulos paralelos e perpendiculares.
- Compreenda algumas estatísticas básicas. Na pré-álgebra, sua introdução à estatística geralmente inclui elementos visuais, como gráficos, gráficos de dispersão, gráficos de estampagem e histogramas.
- Aprenda o básico de álgebra. Isso inclui conceitos como resolver equações simples contendo variáveis, aprender sobre propriedades como a propriedade distributiva, desenhar equações simples e resolver desigualdades.
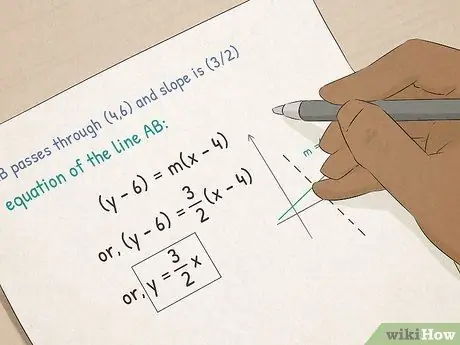
Etapa 3. Avance para Álgebra I
Em seu primeiro ano de álgebra, você aprenderá sobre os símbolos básicos incluídos na álgebra. Você também aprenderá a:
- Resolva equações e inequações contendo variáveis. Você aprenderá como resolver esses problemas no papel e como resolvê-los com fotos.
- Resolva problemas de história. Você ficará surpreso com a quantidade de problemas diários que enfrentará no futuro, que exigem a habilidade de resolver problemas algébricos de histórias. Por exemplo, você usaria a álgebra para descobrir a taxa de juros que ganha em sua conta bancária ou investimento. Você também pode usar a álgebra para descobrir quanto tempo deve viajar com base na velocidade do seu carro.
- Trabalhe com expoentes. Ao começar a resolver equações polinomiais (expressões que contêm números e variáveis), você entenderá como usar expoentes. Isso provavelmente incluirá exercícios com notação científica. Depois de dominar os expoentes, você pode aprender a adicionar, subtrair, multiplicar e dividir expressões polinomiais.
- Resolva problemas de raiz quadrada e quadrada. Ao dominar este tópico, você será capaz de memorizar os quadrados de muitos números. Você também poderá trabalhar com equações que possuem raízes quadradas.
- Compreenda funções e gráficos. Na álgebra, você aprenderá sobre equações gráficas. Você aprenderá como calcular a inclinação de uma linha, como colocar uma equação na forma de inclinação de ponto e como calcular a fatia xey de uma linha usando a forma de inclinação-interceptação.
- Descubra o sistema de equações. Às vezes, você recebe 2 equações diferentes com as variáveis xey e precisa resolver para x ou y para ambas as equações. Felizmente, você aprenderá muitos truques para resolver essas equações, incluindo gráficos, substituição e adição.

Etapa 4. Estudo da geometria
Em geometria, você aprenderá sobre as propriedades de linhas, segmentos, ângulos e formas.
- Você memorizará vários teoremas e corolários que o ajudarão a entender as regras da geometria.
- Você aprenderá como calcular a área de um círculo, como usar o teorema de Pitágoras e como encontrar a relação entre os ângulos e os lados de um triângulo especial.
- Você verá muitas questões de geometria em futuros testes padronizados, como SAT, ACT e GRE.
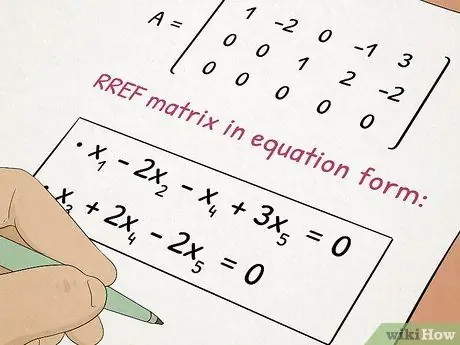
Etapa 5. Faça a aula de Álgebra II
Álgebra II baseia-se nos conceitos que você aprendeu em Álgebra I enquanto adiciona tópicos complexos, como equações quadráticas e matrizes.
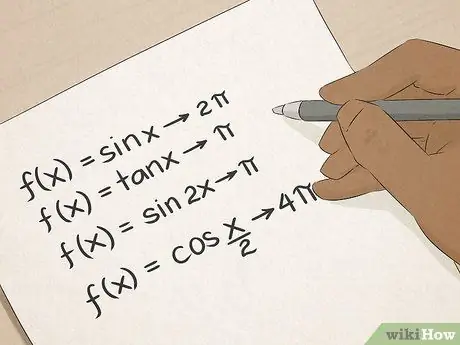
Etapa 6. Dominar a trigonometria
Você conhece os termos trigonométricos: seno, cosseno, tangente e assim por diante. A trigonometria lhe ensinará muitas maneiras práticas de calcular ângulos e comprimentos de linha, e essas habilidades serão inestimáveis para quem trabalha em construção, arquitetura, engenharia ou agrimensura.
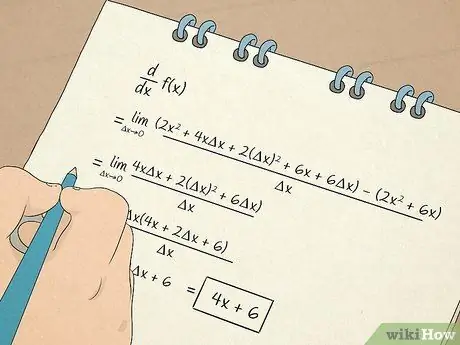
Etapa 7. Faça cálculos de cálculo
O cálculo pode parecer intimidante, mas é uma ferramenta maravilhosa para entender o comportamento dos números ou do mundo ao seu redor.
- Cálculo vai te ensinar funções e limites. Você verá o comportamento do número de funções úteis, incluindo e ^ xe funções logarítmicas.
- Você também aprenderá a calcular e trabalhar com derivadas. A primeira derivada fornece informações com base na inclinação da reta tangente a uma equação. Por exemplo, uma derivada informa a taxa em que algo muda em uma situação não linear. A segunda derivada dirá se a função aumenta ou diminui em um determinado intervalo, para que você possa determinar a concavidade de uma função.
- Os integrais irão ensiná-lo a calcular a área sob uma curva, bem como seu volume.
- O cálculo na escola geralmente termina em sequências e sequências. Embora os alunos não vejam muitas aplicações para circuitos, os circuitos são importantes para quem estuda equações diferenciais.
Parte 3 de 6: Fundamentos da matemática - Adição mestre

Etapa 1. Comece com fatos "+1"
Adicionar 1 a um número leva você ao número mais alto na reta numérica. Por exemplo, 2 + 1 = 3.
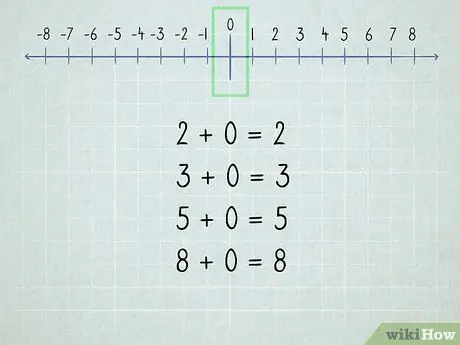
Etapa 2. Entenda o zero
Todos os números adicionados a zero são o mesmo número porque "zero" significa "nenhum".

Etapa 3. Aprenda números duplos
Vários números é um problema que envolve a adição de dois números iguais. Por exemplo, 3 + 3 = 6 é um exemplo de uma equação envolvendo vários números.

Etapa 4. Use o mapeamento para aprender sobre outras soluções de adição
No exemplo abaixo, você aprende mapeando o que acontece quando você adiciona 3 a 5, 2 e 1. Experimente o problema "adicionar por 2" você mesmo.

Etapa 5. Continue até que o número seja superior a 10
Aprenda a somar 3 números para obter um número maior que 10.
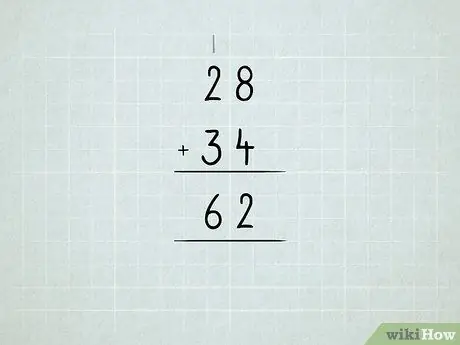
Etapa 6. Some os números maiores
Aprenda sobre como reagrupar unidades em dezenas, dezenas em centenas e assim por diante.
- Some os números da coluna da direita primeiro. 8 + 4 = 12, o que significa que você tem 1 número 10 e 2 número 1. Escreva o número 2 na coluna de unidades.
-
Escreva o número 1 na coluna das dezenas.
-
Some a coluna dezenas em sua totalidade.
Parte 4 de 6: Fundamentos matemáticos - Estratégias de redução

Etapa 1. Comece com "retroceder 1 dígito
Subtrair 1 de um número retorna 1 número. Por exemplo, 4 - 1 = 3.

Etapa 2. Aprenda a subtrair números duplos
Por exemplo, você adiciona os números 5 + 5 para obter 10. Basta escrever a equação ao contrário para obter 10 - 5 = 5.
- Se 5 + 5 = 10, então 10 - 5 = 5.
-
Se 2 + 2 = 4, então 4 - 2 = 2.

Etapa 3. Memorize a família de fatos
Como um exemplo:
- 3 + 1 = 4
- 1 + 3 = 4
- 4 - 1 = 3
- 4 - 3 = 1

Etapa 4. Encontre os números que faltam
Por exemplo, _ + 1 = 6 (a resposta é 5).

Etapa 5. Memorize o fato da subtração em 20

Etapa 6. Pratique subtrair números de 1 dígito de números de 2 dígitos sem pedir emprestado
Subtraia os números da coluna das unidades e diminua os números da coluna das dezenas.
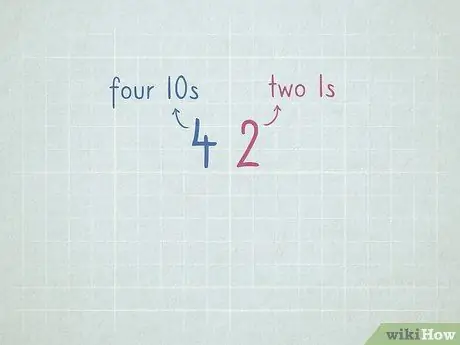
Etapa 7. Pratique o valor posicional para se preparar para subtrair por meio de empréstimo
- 32 = 3 números 10 e 2 números 1.
- 64 = 6 números 10 e 4 números 1.
- 96 = _ número 10 e _ número 1.
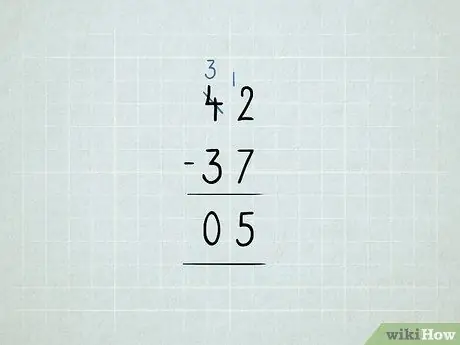
Etapa 8. Subtraia por empréstimo
- Você quer subtrair 42 - 37. Comece tentando subtrair 2 - 7 na coluna de unidades. Acontece que não funcionou!
-
Pegue emprestado o número 10 da coluna das dezenas e coloque-o na coluna das unidades. Agora você tem 3 10 em vez de 4 10. Agora você tem 12 1 em vez de 2 1.
-
Subtraia a coluna das unidades primeiro: 12 - 7 = 5. Em seguida, verifique a coluna das dezenas. Como 3 - 3 = 0, você não precisa anotar o número 0. Sua resposta é 5.
Parte 5 de 6: Fundamentos da matemática - Multiplicação Mestre

Etapa 1. Comece com o número 1 e o número 0
Todos os números multiplicados por 1 são iguais ao próprio número. Qualquer número multiplicado por 0 é igual a zero.

Passo 2. Memorize a tabuada

Etapa 3. Pratique com problemas de multiplicação de um dígito

Etapa 4. Multiplique o número de 2 dígitos pelo número de 1 dígito
- Multiplique o número inferior direito pelo número superior direito.
-
Multiplique o número inferior direito pelo número superior esquerdo.
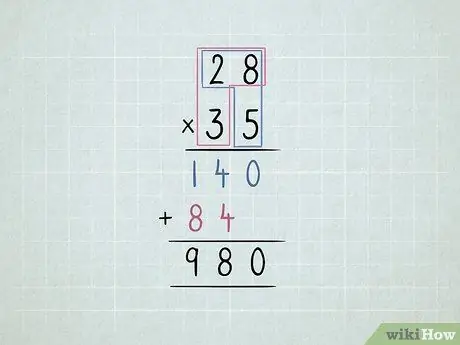
Etapa 5. Multiplique 2 números de 2 dígitos
- Multiplique o número inferior direito pelo número superior direito e, a seguir, pelo número superior esquerdo.
-
Mova a segunda linha um dígito para a esquerda.
- Multiplique o número inferior esquerdo pelo número superior direito e, em seguida, o número superior esquerdo.
-
Some todas as colunas.
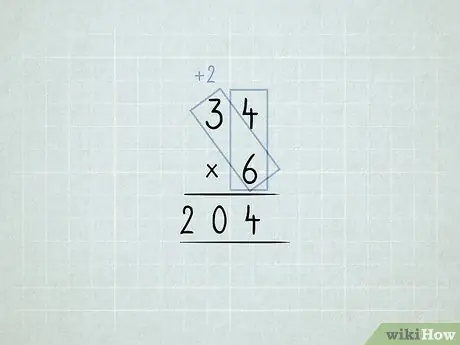
Etapa 6. Multiplique e reagrupe as colunas
- Você quer multiplicar 34 x 6. Você começa multiplicando a coluna de unidades (4 x 6), mas não pode ter 24 1s na coluna de unidades.
-
Armazene 4 1s na coluna de unidades. Mova 2 10s para a coluna das dezenas.
-
Multiplique 6 x 3, que é igual a 18. Some o 2 que você moveu, que é igual a 20.
Parte 6 de 6: Fundamentos matemáticos - revelar problemas de divisão

Etapa 1. Pense na divisão em oposição à multiplicação
# * Se 4 x 4 = 16, então 16/4 = 4.
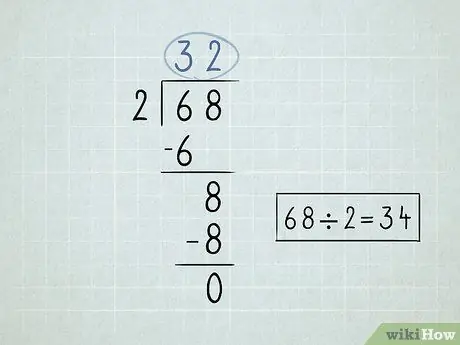
Etapa 2. Anote seu problema de divisão
- Divida o número à esquerda do símbolo de divisão, ou divisor, pelo primeiro número abaixo do símbolo do divisor. Como 6/2 = 3, você escreveria o número 3 acima do símbolo de divisão.
-
Multiplique o número acima do símbolo de divisão pelo divisor. Traga o resultado para a parte inferior do primeiro número sob o símbolo de divisão. Como 3 x 2 = 6, você diminuirá o número 6.
- Subtraia os 2 números que você anotou. 6 - 6 = 0. Você pode deixar 0 em branco, porque geralmente não inicia os números com 0.
-
Traga para baixo o segundo número que está abaixo do símbolo de divisão.
- Divida o número que você reduz pelo divisor. Nesse caso, 8/2 = 4. Escreva o número 4 acima do símbolo de divisão.
-
Multiplique o número superior direito pelo divisor e traga o número para baixo. 4 x 2 = 8.
-
Subtraia esses números. A subtração final retorna zero, o que significa que você resolveu o problema. 68 x 2 = 34.

Etapa 3. Calcule também o restante
Alguns dos divisores não estão totalmente divididos em outros números. Se você completou a última subtração e não tem mais números para derivar, o último número é o resto.






