- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:13.
- Última modificação 2025-01-23 12:43.
As bolas de bilhar se chocam com uma elasticidade perfeita. Ou seja, a energia cinética do movimento é quase completamente preservada e muito pouco dela é convertida em calor ou outra energia. Isso torna o bilhar um esporte interessante para ser analisado matematicamente. Se você tiver controle total sobre como cutuca a bola branca e para onde ela vai, sempre será capaz de prever o que acontecerá.
Etapa
Parte 1 de 3: Predizendo o ângulo de salto da bola no trilho
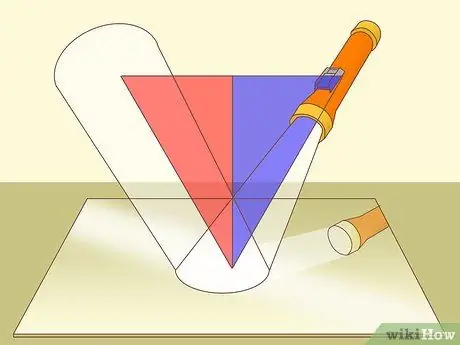
Etapa 1. Compreenda a lei da reflexão
Muitos jogadores de sinuca já conhecem essa matemática simples porque ela é necessária toda vez que eles querem quicar a bola nos trilhos (bordas acolchoadas na mesa de sinuca). Esta lei estabelece que o ângulo de incidência do reflexo é igual ao ângulo de partida. Ou seja, se a bola atingir o trilho em um ângulo de 30º, o ângulo de salto também será de 30º.
A lei da reflexão originalmente se referia à natureza da luz. Normalmente, esta lei diz "O ângulo de incidência é igual ao ângulo de reflexão."
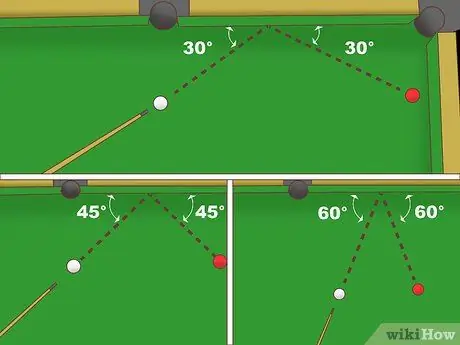
Etapa 2. Defina a bola branca e a bola objeto na mesma distância do trilho
Nesse cenário, seu objetivo é quicar a bola branca no trilho e acertar a bola-objeto. Agora, tente aplicar as seguintes técnicas básicas de geometria:
- Desenhe uma linha de sombra da bola branca que é perpendicular ao corrimão. Esta é a primeira linha.
- Em seguida, imagine o caminho do reflexo da bola branca em direção à grade. Esta linha é a hipotenusa (hipotenusa) de um triângulo retângulo formado a partir da primeira linha e do trilho.
- Agora, imagine a bola branca quicando no trilho e atingindo a bola-objeto. Suponha que haja um segundo triângulo retângulo na esfera do objeto que é simétrico ao primeiro triângulo.
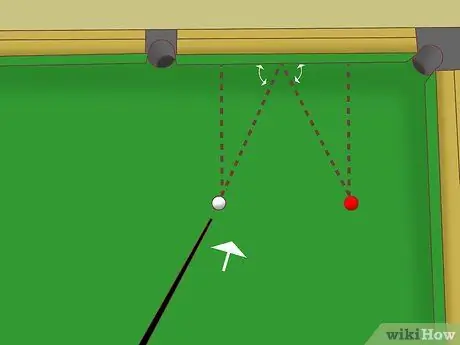
Etapa 3. Prove que esses dois triângulos são congruentes
Nesse caso, podemos usar a regra do "ângulo lateral". Se os dois triângulos tiverem dois ângulos iguais e um lado for o mesmo (na mesma configuração), os dois triângulos são congruentes. (Em outras palavras, a forma e o tamanho são iguais). Podemos provar se esses dois triângulos na mesa de bilhar satisfazem estas condições:
- A lei da reflexão afirma que os dois ângulos entre a hipotenusa e o trilho têm a mesma medida.
- Ambos são ângulos retos, então cada um tem um ângulo de 90º.
- Como as duas bolas estão à mesma distância do trilho, os dois lados entre a bola e o trilho têm o mesmo comprimento.
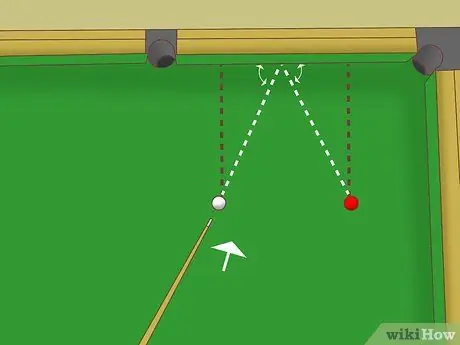
Etapa 4. Mire no ponto médio do trilho
Como esses dois triângulos são congruentes, os comprimentos dos lados dos trilhos também são iguais. Ou seja, a distância do ponto de salto até as duas bolas é a mesma. Mire para o ponto médio se a bola branca e a bola objeto estiverem à mesma distância da grade.
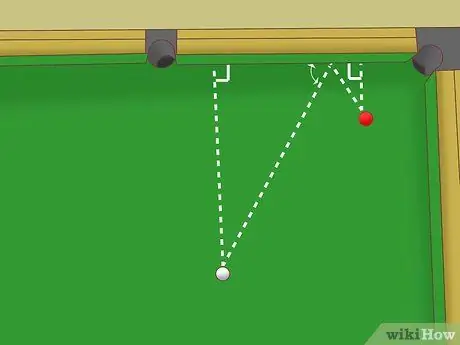
Etapa 5. Use um triângulo semelhante se a bola branca e a bola objeto não estiverem à mesma distância do trilho
Digamos que a distância da bola branca à grade seja duas vezes a distância da bola objeto à grade. Você ainda pode imaginar os dois triângulos retângulos formados pelo caminho ideal da esfera branca e usar sua intuição geométrica para mirar:
- Os dois triângulos ainda têm os mesmos ângulos, mas comprimentos laterais diferentes. Ou seja, os dois triângulos ainda são semelhantes: a forma é a mesma, mas o tamanho é diferente.
- Como a bola branca está duas vezes mais longe do trilho, o primeiro triângulo é duas vezes maior que o segundo triângulo.
- Ou seja, o lado do trilho do primeiro triângulo é duas vezes mais longo que o lado do trilho do segundo triângulo.
- Neste caso, aponte para um ponto no trilho na distância da bola objeto porque é o dobro.
Parte 2 de 3: Calculando o Ângulo de Impacto de Objetos de Bola
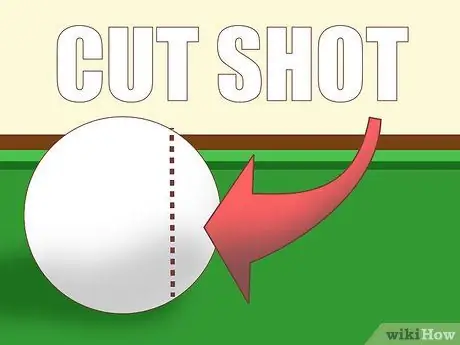
Etapa 1. Aprenda o básico
A maioria dos golpes no bilhar são arremessos de canto ou "cortes", o que significa que a bola branca não atinge o objeto diretamente. Quanto mais "fina" a bola atingir, maior será o ângulo do caminho da bola do objeto, dependendo da trajetória da bola branca.
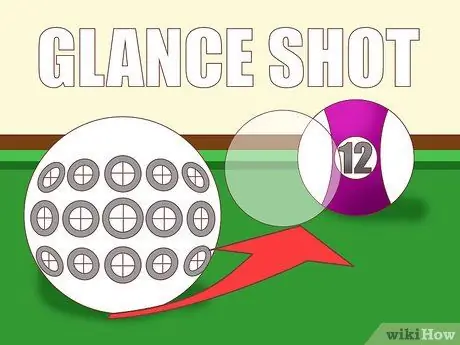
Etapa 2. Estime a plenitude do impacto
Uma boa maneira de estimar esse efeito é monitorar o impacto em relação à trajetória planejada da bola. Quando as bolas colidem, quanto a bola branca "se sobrepõe" à bola objeto de sua perspectiva? A resposta mostrará o quão "total" a bola atingiu:
- Ons mortos se sobrepõem completamente. Você poderia dizer que o nível de "plenitude" é 1.
- Se a bola branca cobrir as bolas do objeto, significa que a colisão das bolas está completa.
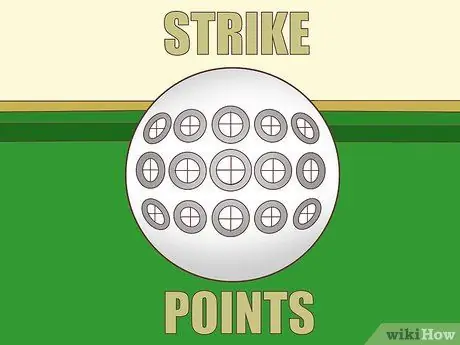
Etapa 3. Estime o ângulo com base no grau de plenitude
Os gráficos dessas duas quantidades não são totalmente lineares, mas próximos o suficiente para que você possa estimá-los adicionando 15º cada vez que você subtrair a plenitude. Caso contrário, você pode usar as seguintes medidas, que são mais precisas:
- O impacto direto (1º grau de preenchimento) resulta em um ângulo de corte de 0º. A bola objeto continua completamente o caminho da bola branca.
- Um impacto total envia a bola-objeto em um ângulo de 14,5º.
- Um impacto total envia a bola-objeto em um ângulo de 30º.
- Uma colisão total envia a bola-objeto em um ângulo de 48,6º.
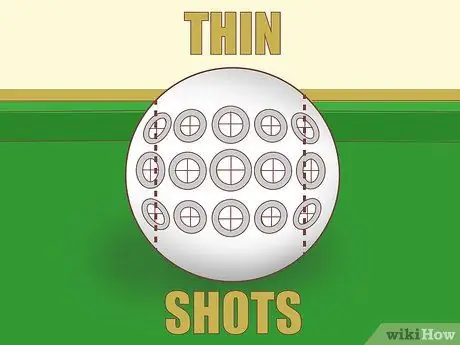
Etapa 4. Tenha cuidado ao fotografar com pouca espessura
Se você quiser acertar a bola com menos de, é difícil estimar o número de bolas cobertas. Além do mais, o impacto do ângulo de corte é tão drástico que um pequeno erro mudará muito o ângulo resultante. Essa foto tangente requer muita prática e funciona bem quando você sabe o ponto que está mirando. Se você puder, encontre outra foto para tirar.
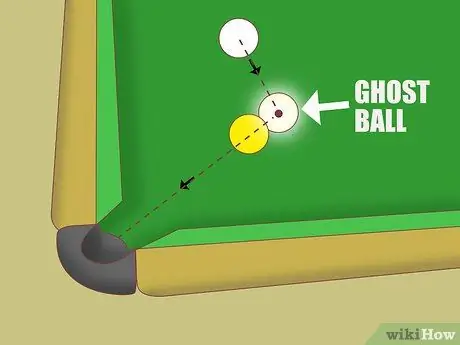
Etapa 5. Tente aplicar o método da bola fantasma para mirar
Se a descrição da plenitude do impacto não ajudar você, tente a abordagem de "bola fantasma":
- Imagine que há uma linha reta da caçapa da mesa até o centro da bola objetiva.
- Estenda esta linha ligeiramente além da bola do objeto. Imagine que existe uma “bola fantasma” neste ponto, estando na linha e tocando a bola objeto.
- Para jogar a bola objeto no bolso, você precisa apontar para o centro da "bola fantasma".
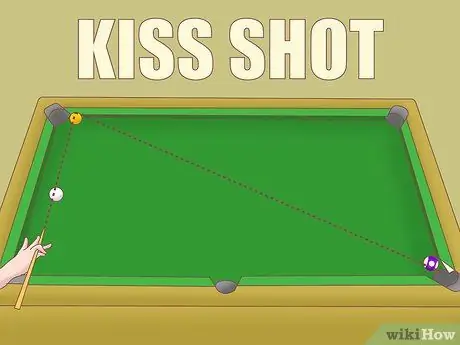
Etapa 6. Aplique a terceira regra de fotos de beijo
Uma tacada é feita ao acertar uma bola branca contra a bola A para que ela mire e acerte a bola B. Se você estiver jogando um jogo em que beijos são permitidos, mantenha esta regra em mente: se a bola A atingir a grade, o ângulo de corte você aponta para o ângulo formado pelas três bolas.
Por exemplo, se o ângulo com a esfera A como vértice é 45º, o ângulo de corte é cerca de 15º. A regra de plenitude acima afirma que este ângulo pode ser produzido com uma colisão total
Parte 3 de 3: Usando o inglês (Side Twist)
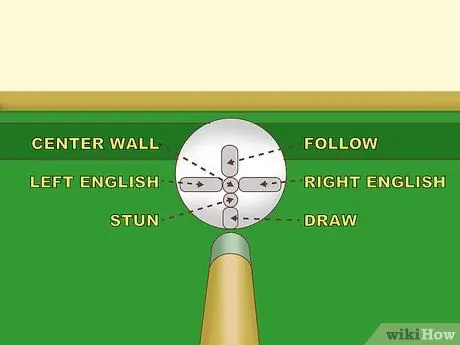
Etapa 1. Aperfeiçoe seu puxão primeiro
Um cutucão com atitude e mira consistentes deve ser uma prioridade se você quiser jogar sinuca seriamente. O inglês é uma técnica muito útil, mas seus efeitos são complexos e você precisa praticá-la consistentemente.
Você terá dificuldade em estreitar o impacto do inglês se não assumir o controle das forças de overspin e deslizamento. Este impacto é determinado pela altura do ponto de impulso da bola. O escorregão pode ser completamente eliminado ao atingir um ponto do comprimento entre o centro e o topo da bola, mas é comum os jogadores atingirem em um ponto desta distância para controle e velocidade ideais
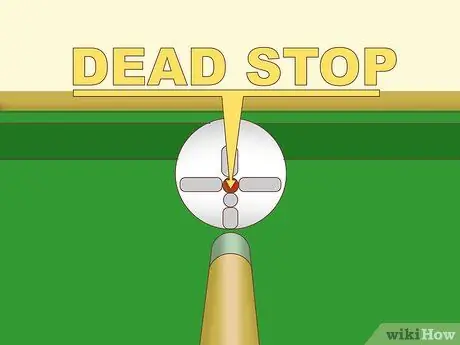
Passo 2. Fique longe do inglês quando a bola branca estiver em perigo de entrar no saco
Desde que não haja inglês, a bola branca irá parar completamente após um impacto direto perfeito. Pratique o impacto direto acertando exatamente no centro dos eixos vertical e horizontal da bola branca. Depois de fazer a bola branca parar completamente a cada vez, você deve ser habilidoso o suficiente para incluir o inglês no jogo.
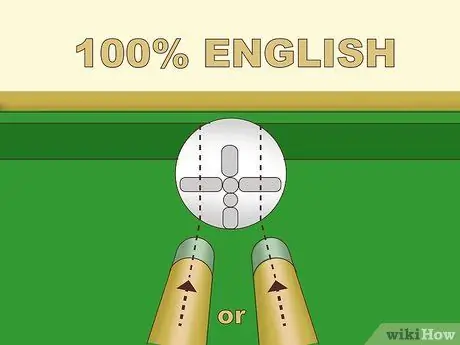
Etapa 3. Pratique vários pontos fortes do inglês
Existem vários tipos de inglês, mas este artigo discute apenas as formas básicas. Se o stick ficasse à esquerda do centro da bola, a bola giraria ao longo desse eixo; aqui está "Inglês esquerdo". Quando esta bola giratória atinge a superfície, o giro fará com que a bola gire mais para a esquerda do que sem o inglês. Inversamente, cutucar à direita do centro da bola branca trará "English right" e fará a bola saltar ainda mais para a direita. Quanto mais longe você cutucar do centro da bola, maior será o impacto:
- Inglês 100% ou máximo é feito cutucando o ponto médio entre o centro e a borda da bola. Esta é a distância máxima de cutucada para conseguir uma cutucada com erro mínimo.
- 50% inglês é feito cutucando o ponto médio entre o ponto máximo e o centro da bola (¼ da distância entre o centro e a borda da bola).
- Você pode usar porcentagens em inglês cutucando vários pontos entre o centro e o ponto máximo da bola branca.
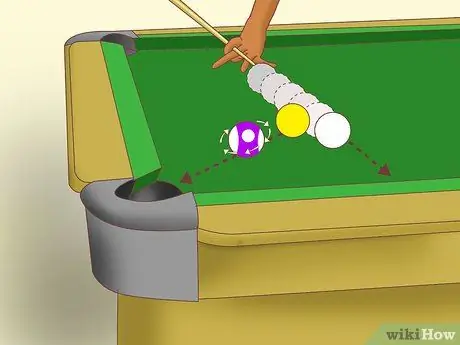
Etapa 4. Compreenda a engrenagem
Quando duas bolas colidem, a bola objeto começa a girar em um determinado eixo, de acordo com o ângulo da tacada e a quantidade de inglês obtida. Se você conseguir "engrenar", essa rotação ocorrerá ao longo do eixo do movimento. Em outras palavras, o movimento da bola objeto não é afetado pela rotação. A bola deslizará ao longo da “linha central” ou a linha desenhada entre os centros das duas bolas no impacto.
O termo vem da analogia de duas engrenagens trabalhando suavemente uma com a outra e transmitindo o movimento perfeitamente
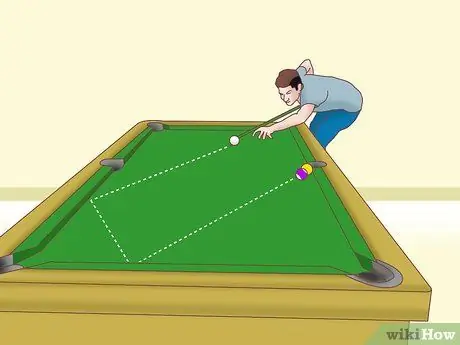
Etapa 5. Ajuste o inglês para obter a engrenagem em todas as peças
Depois de acertar um canto usando a abordagem "cheia" ou "bola fantasma", é uma boa ideia certificar-se de que a bola objeto não gire de maneira estranha e prejudique a tacada. Aqui está um gráfico que pode ajudá-lo a encontrar o ângulo certo e o inglês. Todos os números abaixo são "Inglês fora", o que significa que você move o stick próximo à bola branca além da bola objeto.
- Se o ângulo de corte for 15º, use o inglês ligeiramente maior que 20%. (Lembre-se de que o ângulo de corte é o ângulo entre o caminho inicial da bola branca e o caminho da bola do objeto.)
- Se o ângulo de corte for 30º, use o inglês a 40%.
- Se o ângulo de corte for 45º, use 55% do inglês.
- Se o ângulo de corte for 60º, use o inglês a 70%.
- Quando o ângulo de corte se aproximar de 90º, aumente o inglês para 80%.
Etapa 6. Conheça o efeito do impacto sem engrenagens
Se voce usa ingles menos Das muitas "engrenagens" da última etapa, a bola branca se deslocará para a frente durante o impacto e a torção lateral se deslocará para a bola-objeto. Em seguida, a bola do objeto se moverá ligeiramente para a direita do ângulo de corte estimado. Se o seu inglês for mais do que engrenagens, a bola do objeto se moverá ligeiramente para a esquerda do ângulo de corte estimado.
- Esse efeito é chamado de lance induzido por corte: o ângulo do corte desloca a torção que faz com que a bola role ligeiramente para fora do curso.
- Você pode usar essa técnica para fazer tomadas que parecem quase impossíveis. Se sua única tacada for um pouco longe demais para a direita, aumente seu inglês para colocar a bola na caçapa.
Pontas
- Se a bola objeto estiver presa ao trilho e você precisar rolar ao longo do trilho em direção ao saco, sempre bata no trilho antes de tocar na bola objeto. Assim, a bola branca dá impulso ao trilho, ao invés de em direção a ele. (Se o ângulo de impacto exceder 45º, você precisará usar o inglês.)
- Quanto maior o ângulo de impacto entre as duas bolas, menor será o momento transmitido. Isso significa que você precisará cutucar um pouco mais forte para cortes finos (rachaduras em ângulos extremos).
- Após o impacto, o ângulo entre a trajetória da bola branca e a trajetória da bola do objeto deve ser sempre igual a 90º. Use esse conhecimento para evitar que as bolas brancas entrem no saco. Observe que a torção extrema pode quebrar esta regra, e bolas de diferentes massas (por exemplo, em uma mesa de bilhar comum em um café).






