- Autor Jason Gerald [email protected].
- Public 2023-12-16 11:33.
- Última modificação 2025-01-23 12:43.
Contar frações é uma das habilidades matemáticas mais úteis para desenvolver. Antes de fazer cálculos fracionários, aprenda como identificar partes e tipos de frações. Depois disso, você pode adicioná-los ou subtraí-los. Para cálculos mais complexos, aprenda como multiplicar e dividir frações. Normalmente, você também precisará simplificar ou reduzir as frações.
Etapa
Método 1 de 4: Reconhecendo Frações

Etapa 1. Encontre a fração
As frações são escritas como um número acima da linha divisória e outro número abaixo da linha.
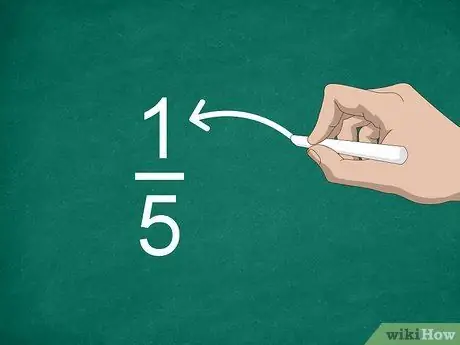
Etapa 2. Identifique o numerador
O número acima da linha é chamado de numerador e mostra quantas partes existem na fração.
Por exemplo, na fração 1/5, “1” é o numerador
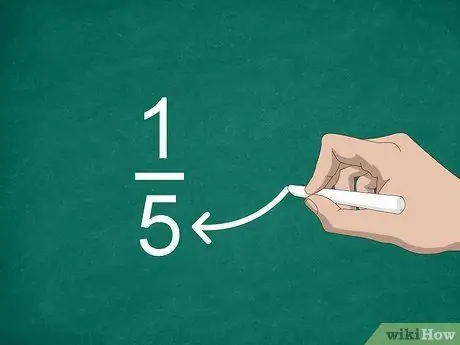
Etapa 3. Encontre o denominador
O número colocado abaixo da linha é chamado de denominador. Este valor indica o número de partes que "constroem" um inteiro.
Por exemplo, na fração 1/5, "5" é o denominador, portanto, há cinco partes para a fração

Etapa 4. Determine se as frações são frações razoáveis ou frações impróprias
Se o numerador for menor que o denominador, a fração é uma fração natural. Em frações impróprias, o numerador é maior que o denominador.
- Por exemplo, 3/4 é uma fração razoável e 5/3 é uma fração imprópria.
- Se você tiver um número inteiro que inclui uma fração, o número é conhecido como um número misto. Por exemplo, 1 1/2 é um número misto.
Método 2 de 4: adicionar ou subtrair frações

Etapa 1. Identifique as frações com o mesmo denominador
Se você precisar adicionar ou subtrair frações, cada fração deve ter o mesmo denominador antes de realizar o cálculo. Observe o denominador de cada fração para certificar-se de que todas são iguais (semelhantes).
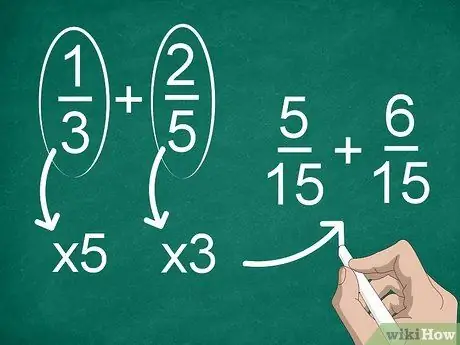
Etapa 2. Encontre um denominador comum se cada fração tiver um denominador diferente
Se os denominadores não forem iguais, você precisará alterar as frações para que tenham o mesmo denominador. Para encontrar um denominador comum, multiplique cada fração pelo denominador da outra.
Por exemplo, para encontrar um denominador comum em 1/3 + 2/5, multiplique “1” e “3” por “5” e, em seguida, multiplique “2” e “5” por “3”. Agora, você tem a adição de 5/15 + 6/15. Depois disso, você pode calcular as frações
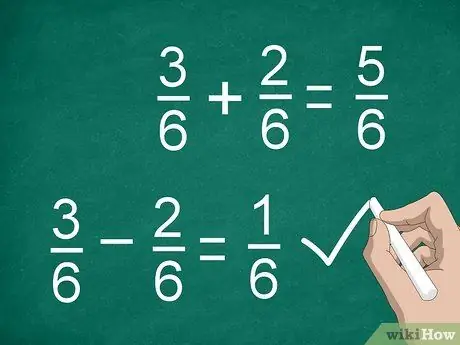
Etapa 3. Adicione ou subtraia os numeradores para calcular as frações
Depois de encontrar um denominador comum e multiplicar os numeradores (se necessário), você está pronto para somar ou subtrair. Adicione ou subtraia os numeradores e coloque o resultado acima da linha divisória. Escreva o denominador comum abaixo da linha.
- Por exemplo, 3/6 - 2/6 = 1/6.
- Não adicione ou subtraia os denominadores.
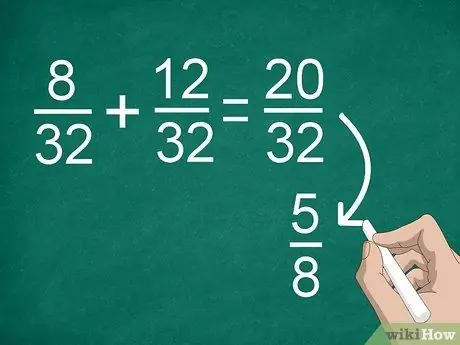
Etapa 4. Simplifique os resultados, se necessário
Se você precisava encontrar um denominador comum anteriormente, pode obter uma grande fração que pode simplificar. Por exemplo, se você adicionar 8/32 +12/32, obterá “20/32” como resultado. Esta fração pode ser simplificada para “5/8”.
Método 3 de 4: Multiplicando e Simplificando Frações
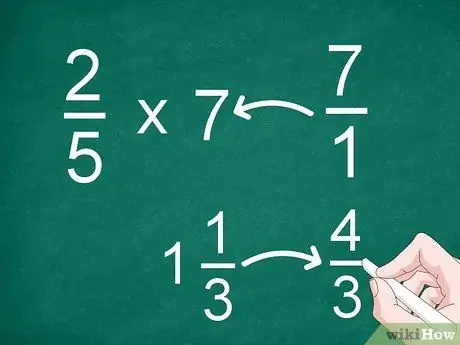
Etapa 1. Converta frações mistas ou inteiros em frações impróprias
Para tornar a multiplicação mais fácil, você precisa converter cada número em uma fração razoável ou imprópria. Se você tiver números inteiros ou mistos que precisam ser multiplicados, primeiro converta-os em uma fração comum (natural ou imprópria).
- Por exemplo, para multiplicar 2/5 por 7, converta "7" em uma fração. Depois disso, você pode multiplicar 2/5 por 7/1.
- Se você tiver um número misto como 1 1/3, converta-o em uma fração imprópria (“4/3”) antes de multiplicar.
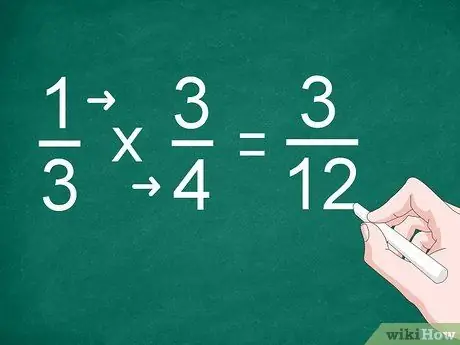
Etapa 2. Multiplique cada numerador e denominador
Em vez de fazer a adição, multiplique o numerador e escreva o resultado acima da linha divisória. Você também precisa multiplicar os denominadores e escrever o resultado abaixo da linha.
Por exemplo, para multiplicar 1/3 por 3/4, multiplique “1” por “3” para obter o numerador. Multiplique “3” por “4” para obter o denominador. A resposta para a multiplicação é "3/12"

Etapa 3. Simplifique os resultados
Normalmente, você precisará reduzir o resultado para uma forma mais simples, especialmente se inicialmente tiver frações não naturais. Encontre o maior fator comum e use esse fator para simplificar o numerador e o denominador.
Por exemplo, para a fração 3/12, o maior fator comum entre “3” e “12” é “3”. Divida cada elemento da fração por “3” até obter a fração “1/4”
Método 4 de 4: dividir frações
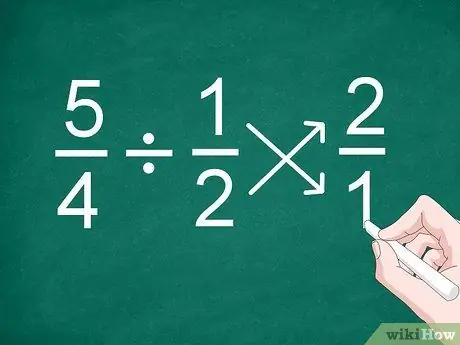
Etapa 1. Inverta a posição da segunda fração
A maneira mais fácil de dividir frações, mesmo frações com denominadores diferentes, é inverter a posição da segunda fração antes de calcular o resultado.
Por exemplo, para o problema 5/4 1/2, inverta a posição da fração “1/2” para se tornar “2/1”
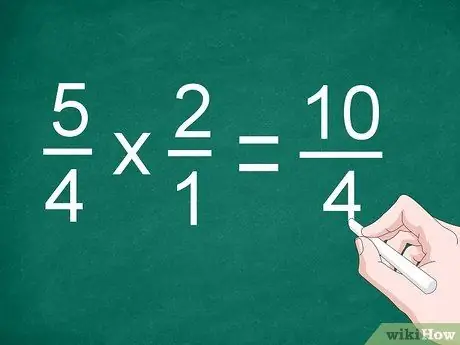
Etapa 2. Multiplique o numerador e o denominador
Multiplique as frações diretamente para multiplicar os numeradores. Escreva o resultado acima da linha divisória e multiplique o denominador. Registre o produto dos denominadores abaixo da linha.
Para o exemplo anterior, multiplique 5/4 por 2/1 para obter “10/4”
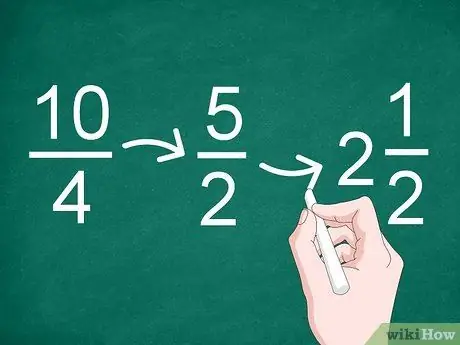
Etapa 3. Simplifique os resultados, se necessário
Se o resultado da divisão for uma fração imprópria ou puder ser reduzido, simplifique a fração. Use o maior fator comum para reduzir a fração.
- Por exemplo, o maior fator comum na fração 10/4 é “2”, então o resultado da simplificação torna-se “5/2” (10 dividido por 2 e 4 dividido por 2).
- Como o resultado da simplificação é uma fração imprópria, você pode convertê-lo em um inteiro e uma fração (um número misto). Portanto, 5/2 pode ser alterado para “2”.
Pontas
- Se estiver trabalhando com frações complexas, você precisará realizar algumas etapas adicionais para simplificar a fração. No entanto, esta simplificação em si é uma parte obrigatória do processo de cálculo.
- Sempre escreva as frações de maneira organizada para reduzir o risco de erros de cálculo.






