- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2023-12-16 11:33.
- Última modificação 2025-01-23 12:43.
Para a maioria das pessoas, as frações são os primeiros cálculos complicados que aparecem. O conceito de frações é bastante difícil e requer que você aprenda condições especiais para fazê-lo. Como as frações têm regras especiais para adição, subtração, multiplicação e divisão, muitas pessoas ficam confusas. Porém, com muita prática, qualquer pessoa pode aprender e fazer cálculos relacionados às frações.
Etapa
Método 1 de 5: Compreendendo as frações
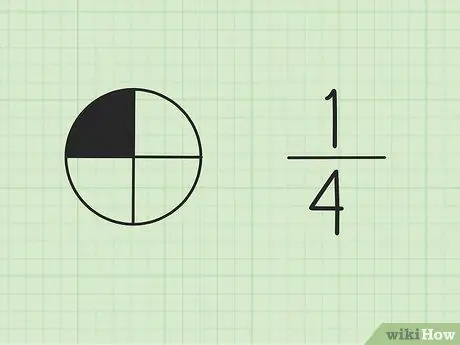
Etapa 1. Entenda que as frações fazem parte de um todo
O número na parte superior é chamado de numerador e representa o número de partes do total. O número na parte inferior é chamado de denominador, que representa o número total de peças.
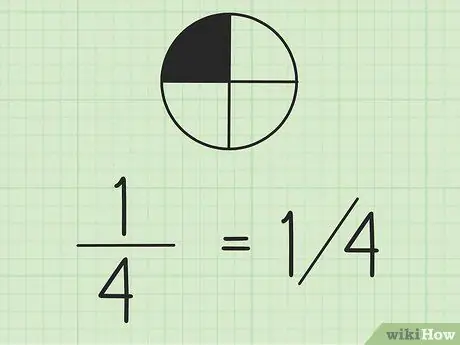
Etapa 2. Lembre-se de que você pode escrever frações usando barras
O número à esquerda é o numerador e o número à direita é o denominador. Se você estiver trabalhando com frações na mesma linha, é uma boa ideia escrever o numerador acima do denominador.
Por exemplo, se você pegar uma das quatro fatias de pizza, terá pizza. Se você tem 7/3 pizzas, isso significa que você tem duas pizzas inteiras mais 1 de 3 fatias de pizza
Método 2 de 5: diferença entre frações mistas e simples

Etapa 1. Compreenda que os números mistos consistem em números inteiros e frações, por exemplo 2 1/3 ou 45 1/2
Normalmente, você precisa converter números mistos em uma forma mais simples para adicionar, subtrair, multiplicar ou dividir.

Etapa 2. Altere o número misto multiplicando o número inteiro pelo denominador na fração e, em seguida, adicionando-o pelo numerador
Escreva o resultado como o numerador, enquanto o denominador não muda.
Por exemplo, para converter 2 1/3 em uma fração simples, multiplique 2 por 3, some 1 e obtenha 7/3

Etapa 3. Converta frações simples em números mistos, dividindo o numerador pelo denominador
Todo o resultado da divisão é escrito como um inteiro e o restante da divisão é escrito como o numerador da fração. O denominador não muda.
Por exemplo, para converter 7/3 em um número misto, divida 7 por 3 para obter 2 com o resto de 1. Portanto, o número misto é 2 1/3. As frações simples só podem ser convertidas em números mistos se o numerador for maior que o denominador
Método 3 de 5: adição e subtração de frações
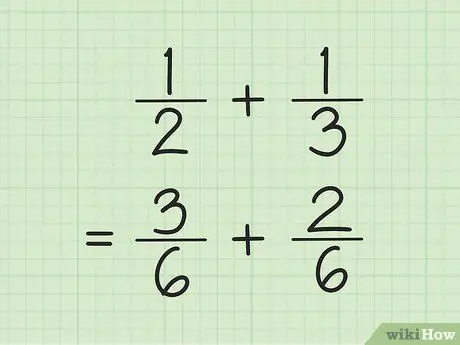
Etapa 1. Encontre um denominador comum para adicionar e subtrair frações
O truque, multiplique os números no denominador e, em seguida, multiplique cada numerador pelo número usado para encontrar o denominador. Às vezes, você pode encontrar o MMC (mínimo múltiplo comum) para o denominador multiplicando os denominadores entre si.
Por exemplo, para somar e 1/3, primeiro encontre o MMC (mínimo múltiplo comum) dos dois denominadores multiplicando-se. Assim, você multiplica 2 e 3 para obter MMC 6. Multiplique 1 por 3 para obter 3 como o novo numerador da primeira fração. Multiplique 1 por 2 para obter 2 como o novo numerador da segunda fração. Suas novas frações são 3/6 e 2/6
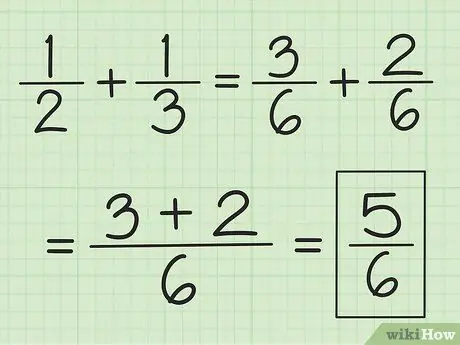
Etapa 2. Adicione os dois numeradores e não altere o denominador
Por exemplo, 3/6 mais 2/6 é 5/6 e 2/6 mais 1/6 é 3/6
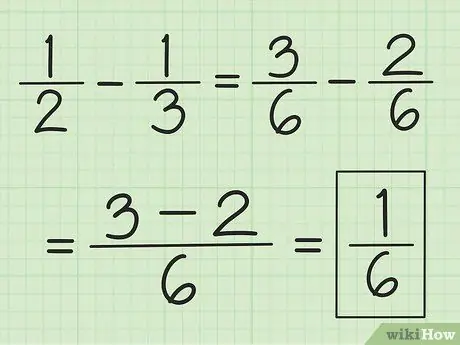
Etapa 3. Use uma técnica semelhante para subtração
Encontre o MMC dos denominadores primeiro, mas em vez de soma-los, subtraia o número do primeiro numerador pelo número do segundo.
Por exemplo, para subtrair 1/3 de 1/2, primeiro altere as frações para 3/6 e 2/6, depois subtraia 3 por 2 para obter 1. Isso resulta em 1/6
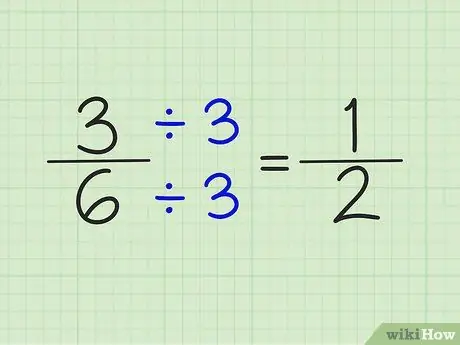
Etapa 4. Simplifique as frações dividindo o numerador e o denominador pelo mesmo número
Por exemplo, o número 5/6 não pode ser simplificado. No entanto, 3/6 pode ser simplificado dividindo o numerador e o denominador pelo número 3. O resultado é uma fração de 1/2

Etapa 5. Converta a fração em um número misto se o numerador for maior que o denominador
Método 4 de 5: multiplique e divida frações
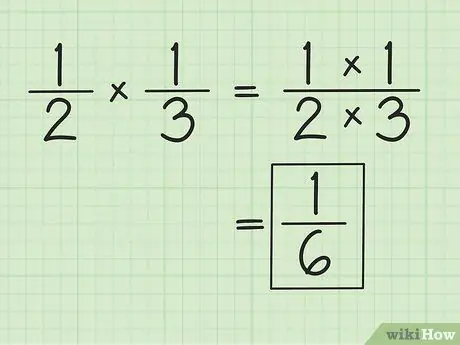
Etapa 1. Multiplique o numerador e o denominador separadamente para multiplicar as frações
Por exemplo, ao multiplicar por 1/3, o resultado é 1/6 (1 vezes 1 e 2 vezes 3). Você não precisa combinar os denominadores ao multiplicar as frações. Simplifique ou modifique os resultados obtidos, se necessário
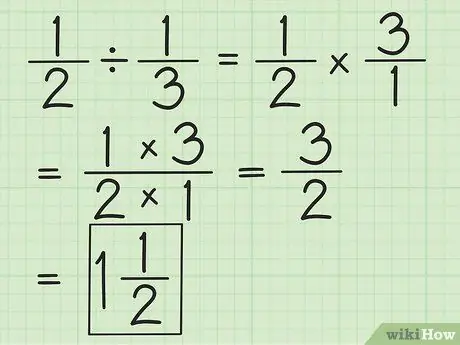
Etapa 2. Divida duas frações invertendo a segunda fração e, em seguida, multiplicando ambas
Por exemplo, se você deseja dividir 1/2 por 1/3, primeiro inverta a segunda fração para 3/1. Multiplique por 3/1 e obtenha 3/2. Simplifique as frações ou converta para números mistos, se possível
Método 5 de 5: Trabalhando com Frações Complexas
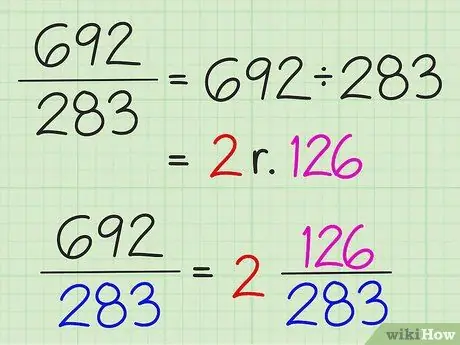
Etapa 1. Trabalhe todas as frações da mesma maneira, mesmo que o problema pareça muito complicado
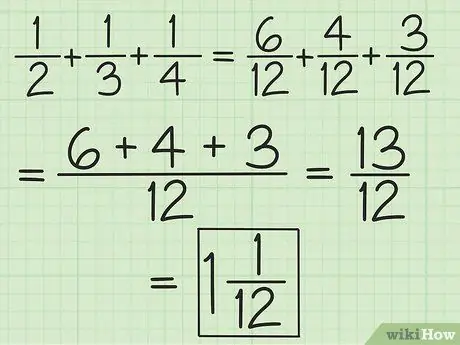
Etapa 2. Combine os denominadores de todas as frações ou trabalhe em pares, começando da esquerda para a direita, para somar e subtrair mais de duas frações
Por exemplo, para adicionar 1/2, 1/3 e 1/4, você pode alterá-los para 6/12, 4/12 e 3/12 para obter 13/12 ou pode adicionar 3/6 e 2 / 6 para obter 5/6 e, em seguida, adicionar 5/6 e 1/4 (equalize os denominadores para que a segunda fração se torne 3/12) para obter 13/12 (10/12 mais 3/12). Converta para um número misto, que é 1 1/12
Pontas
- Lembre-se de que você aprendeu bastante matemática. A matemática é como uma linguagem que você pode pronunciar fluentemente e agora está tentando aprender a ler e escrever.
- Lembre-se de sempre simplificar o resultado final do seu cálculo, seja o seu problema na forma de uma fração comum, um número misto ou uma fração complexa.






