O recíproco ou recíproco é muito útil em todos os tipos de equações algébricas. Por exemplo, ao dividir uma fração por outra, você multiplica a primeira fração pelo recíproco da segunda. Você também precisa usar o inverso ao procurar a equação de uma reta.
Etapa
Método 1 de 3: Encontrando o Inverso de uma Fração ou Inteiro
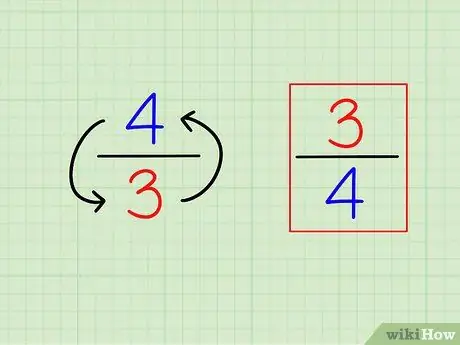
Etapa 1. Encontre o recíproco da fração, invertendo-o
A definição de “recíproco” ou o oposto é muito fácil. Para encontrar o recíproco de qualquer inteiro, simplesmente calcule "1 (esse número)". Para frações, o recíproco é uma fração diferente, ou seja, os números são "invertidos" (inversos).
- Por exemplo, o oposto de 3/4 é 4/3.
- Qualquer número quando multiplicado por seu recíproco retorna 1.
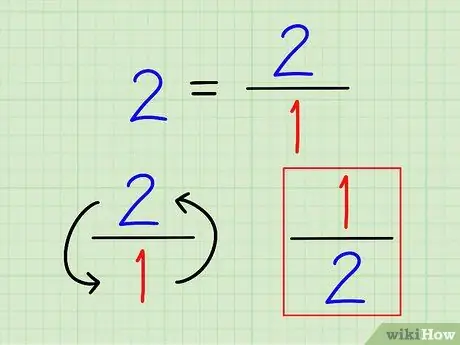
Etapa 2. Escreva o recíproco de todo o número como uma fração
Novamente, o recíproco de um número é sempre 1 (esse número). Para números inteiros, escreva-os como frações. Não faz sentido calcular esse número para uma casa decimal.
Por exemplo, o recíproco de 2 é 1 2 = 1/2.
Método 2 de 3: Encontrando o Inverso de uma Fração Mista
Etapa 1. Identifique números mistos
As frações mistas consistem em números inteiros e frações, como 24/5. Existem duas etapas para encontrar o recíproco de um número misto, conforme descrito abaixo.
Etapa 2. Converta números mistos em frações impróprias
Lembre-se de que 1 sempre pode ser escrito como (número) / (mesmo número) e as frações com o mesmo denominador (número inferior) podem ser somadas. Aqui está um exemplo usando 24/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
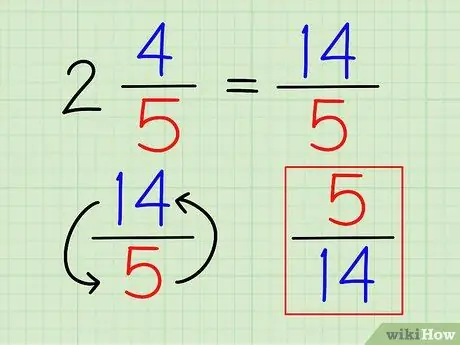
Etapa 3. Vire a fração
Uma vez que o número é escrito completamente como uma fração, você pode encontrar seu recíproco assim como faria com qualquer outra fração, revertendo a fração.
No exemplo acima, o recíproco de 14/5 é 5/14.
Método 3 de 3: Encontrando o Oposto de um Decimal
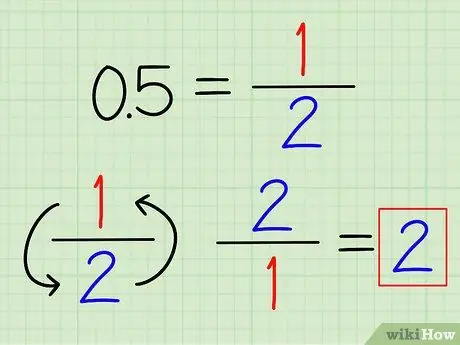
Etapa 1. Converta decimais em frações, se possível
Você pode reconhecer alguns números decimais usados com freqüência, que podem ser facilmente convertidos em frações. Por exemplo, 0,5 = 1/2 e 0,25 = 1/4. Depois que o decimal for convertido em uma fração, basta virar a fração para encontrar seu recíproco.
Por exemplo, o recíproco de 0,5 é 2/1 = 2.
Etapa 2. Escreva um problema de divisão
Se você não pode convertê-lo em uma fração, calcule o recíproco do número na forma de um problema de divisão: 1 (decimal). Você pode usar uma calculadora para resolvê-lo ou prosseguir para a próxima etapa para resolvê-lo manualmente.
Por exemplo, você pode encontrar o recíproco de 0,4 calculando 1 0,4
Etapa 3. Altere o problema de divisão para usar números inteiros
O primeiro passo para dividir decimais é mover o ponto decimal até que todos os números sejam inteiros. Contanto que você mova o ponto decimal de ambos os números no mesmo número de etapas, você obterá a resposta certa.
Por exemplo, você pode usar 1 0, 4 e reescrevê-lo como 10 4. Nesse caso, você move todas as casas decimais um passo para a direita, da mesma forma que multiplica cada número por dez
Etapa 4. Resolva o problema usando a divisão longa
Use o método de divisão longa para calcular o recíproco. Se você contar 10 4, obterá a resposta 2, 5 que é o recíproco de 0, 4.
Pontas
- O recíproco negativo de um número é igual ao recíproco regular, no sentido de que é multiplicado por um negativo. Por exemplo, o recíproco negativo de 3/4 é -4/3.
- O recíproco ou recíproco é freqüentemente referido como o "inverso da multiplicação".
- O número 1 é o oposto de si mesmo porque 1 1 = 1.
- O número 0 não tem recíproco porque 0 é indefinido.
