- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:13.
- Última modificação 2025-01-23 12:43.
Os alunos que ainda são muito jovens muitas vezes têm dificuldade em compreender o conceito de subtração. Se você é professor e deseja ensinar o conceito de subtração aos alunos, tente representar o conceito de uma forma que seja interessante e mais compreensível para os alunos. Depois de explicar os conceitos básicos de subtração, tente passar para o conceito de subtração de dois dígitos. Depois que os alunos tiverem dominado bem, tente explicar vários conceitos que eles podem usar para resolver problemas de subtração, como Common Core.
Etapa
Método 1 de 4: Ensinando subtração por meio de objetos ou imagens

Etapa 1. Escreva ou apresente oralmente um problema de história contendo um problema de subtração para os alunos:
Há 8 laranjas na mesa, 3 laranjas são comidas por Jordan. Quantas laranjas sobraram?
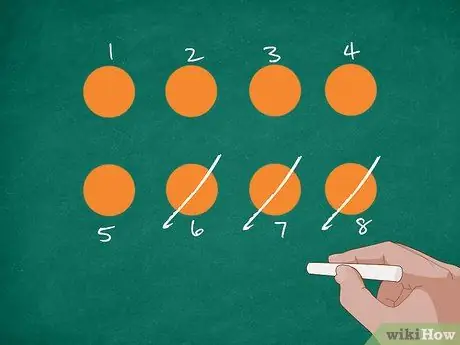
Etapa 2. Represente o problema com fotos
Primeiro, desenhe 8 círculos laranja no quadro ou um pedaço de papel. Depois disso, peça aos alunos que contem o número e rotulem cada círculo com um número. Risque 3 círculos enquanto explica que Jordan comeu 3 laranjas. Pergunte aos alunos quantas laranjas ainda faltam.
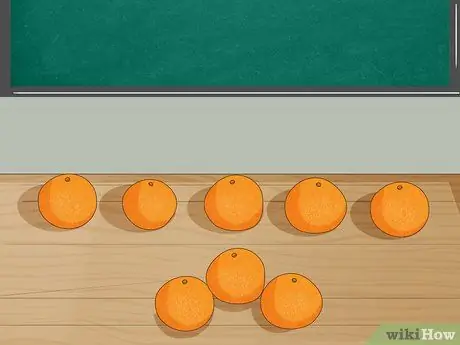
Etapa 3. Represente o problema com objetos
Coloque 8 laranjas na mesa e peça aos alunos que contem o número. Depois disso, pegue 3 laranjas da mesa enquanto explica que Jordan comeu 3 laranjas. Peça aos alunos que contem o número de laranjas restantes.

Etapa 4. Escreva a equação
Explique que os problemas da história também podem ser representados por meio de uma equação. Certifique-se de sempre orientá-los no processo de transformar os problemas da história em equações matemáticas.
- Pergunte quantas laranjas estão na mesa. Escreva o número “8” no quadro.
- Pergunte quantas laranjas Jordan comeu. Escreva o número “3” no quadro.
- Pergunte aos alunos se isso é um problema de adição ou subtração. Escreva um sinal “-” entre os números “8” e “3”.
- Peça aos alunos que procurem respostas para a equação “8-3”. Escreva um sinal “=” seguido do número “5”.
Método 2 de 4: Ensinando Subtração com o Método de Contagem Regressiva na Linha Numérica

Etapa 1. Escreva ou apresente oralmente um problema de história contendo um problema de subtração para os alunos:
Há 10 cães no pet shop, 6 dos quais foram adotados por seus novos donos. Quantos cachorros sobraram no pet shop?
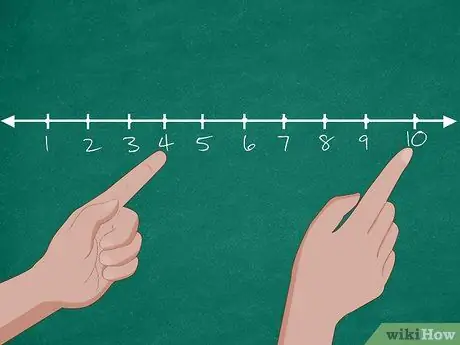
Etapa 2. Use a ajuda de uma linha numérica para resolver o problema
Primeiro, desenhe uma linha numérica contendo os números de 0 a 10 no tabuleiro. Depois disso, peça aos alunos que digam o número de cães na loja de animais. Depois que os alunos responderem, circule o número “10” no quadro. Em seguida, pergunte novamente quantos cães foram adotados. Se os alunos responderem “6”, peça que contem 6 números de 10 (9, 8, 7, 6, 5, 4) até chegarem ao número “4”. Depois disso, pergunte novamente quantos cães sobraram na loja de animais.

Etapa 3. Escreva a equação
Explique que os problemas da história também podem ser representados por meio de uma equação. Certifique-se de sempre orientá-los no processo de transformar os problemas da história em equações matemáticas.
- Pergunte quantos cães há na loja de animais. Escreva o número “10” no quadro.
- Pergunte quantos cães foram adotados. Escreva o número “6” no quadro.
- Pergunte aos alunos se isso é um problema de adição ou subtração. Escreva um sinal “-” entre os números “10” e “6”.
- Peça aos alunos que procurem respostas para a equação “10-6”. Escreva um sinal “=” seguido pelo número “4”.
Método 3 de 4: Ensinando Subtração por meio de Conceitos de Família de Fatos

Etapa 1. Apresente o conceito de família de fatos aos alunos
Na verdade, uma família de fatos é um grupo de problemas matemáticos que consiste nos mesmos números. Por exemplo, os números 10, 3 e 7 formam uma família de fatos. Os três números podem ser adicionados ou subtraídos de maneiras diferentes; Você pode gerar duas equações usando apenas estes 3 números:
- 10-3=7
- 10-7=3
- 7+3=10
- 3+7=10

Etapa 2. Escreva ou apresente verbalmente um problema de história contendo um problema de subtração para os alunos:
Eu tenho 7 doces. Se eu comer 3 doces, quantos doces sobram?

Etapa 3. Use o conceito de família de fatos para resolver o problema
Oriente os alunos pelo processo passo a passo:
- Pergunte aos alunos que problema eles gostariam de resolver. Escreva "7-3 =?" Na lousa.
- Peça-lhes que identifiquem o terceiro membro do grupo familiar de fatos. Escreva as seguintes equações no quadro: “3 + _ = 7”; “_ + 3 = 7”; "; “7 -_ = 3”; e 7-3 = _”Depois disso, peça aos alunos que leiam os resultados e preencham o problema com as respostas que deram.
Método 4 de 4: Apresentando os Conceitos Básicos Comuns
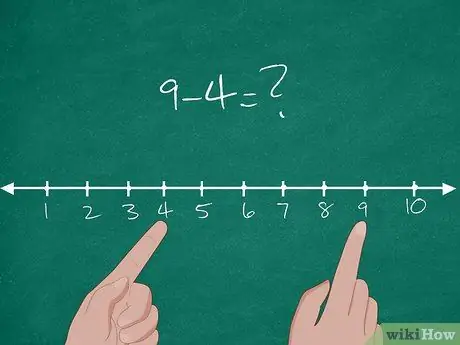
Etapa 1. Ensine o conceito de subtração no Common Core
Na verdade, Common Core é um novo padrão de aprendizagem aplicado pela maioria dos estados da América. No Common Core, o conceito básico de subtração é explicado pela distância entre dois números. Para explicar o conceito aos alunos, tente desenhar uma linha numérica contendo os números de 1 a 10 no quadro.
- Depois disso, dê um problema básico de subtração para os alunos: 9-4 = ?.
- Encontre a localização do número 4 na reta numérica. Explique aos alunos que este local é o ponto de partida.
- Encontre a localização do número 9 na reta numérica. Explique aos alunos que o local é o destino final.
- Depois disso, peça aos alunos para medir ou calcular a distância entre os dois números: “5, 6, 7, 8, 9”.
- A distância entre os dois números é 5. Portanto, 9-4 = 5.
Etapa 2. Peça aos alunos que resolvam o problema de subtração de dois dígitos
Explique aos alunos que haverá dois pontos que eles devem parar antes de chegar ao seu destino.
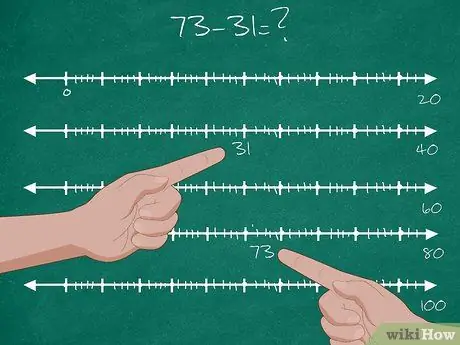
- Dê aos alunos um problema de subtração de dois dígitos: 73-31 = ?.
- Encontre a localização do número 31 na reta numérica. Este é o ponto de partida.
- Encontre a localização do número 73 na linha numérica. Este é o objetivo final.
- “Pare” no primeiro décimo depois de 31. Assim, sua primeira parada é 40. Depois disso, meça a distância entre 31 e 40 e escreva a resposta: 9.
- “Pare” nos décimos que estão mais perto de 73. Assim, sua segunda parada é 70. Em seguida, meça a distância entre 40 (primeira parada) e 70 (segunda parada) e escreva a resposta: 30.
- "Mova-se" de 70 (segunda parada) até seu destino final (73). Meça a distância entre eles e escreva a resposta: 3.
- Some esses três resultados: 9 + 30 + 3 = 42. Assim, 73-31 = 42.

Etapa 3. Peça aos alunos que resolvam o problema de subtração de três dígitos
Ao resolver problemas de subtração de dois dígitos, explique aos alunos que o que vai aumentar não são apenas as escalas, mas também a distância entre cada escala.
- Dê aos alunos um problema de subtração de três dígitos: 815-398 = ?.
- Encontre a localização do número 398 na reta numérica. Este é o ponto de partida.
- Encontre a localização do número 815 na reta numérica. Este é o objetivo final.
- "Pare" no primeiro décimo após 398. Portanto, sua primeira parada é 400. Meça a distância entre 398 e 400 e escreva a resposta: 2.
- "Pare" nos décimos que estão mais perto de 815. Portanto, sua segunda parada é 800. Meça a distância entre 400 e 800 e anote a resposta: 400.
- "Pare" nos décimos que estão mais perto de 815. Portanto, sua terceira parada é 810. Meça a distância entre 800 e 810 e escreva a resposta: 10.
- "Mova-se" da terceira parada até seu destino final, que é o número 815. Meça a distância e anote a resposta: 5.
- Some todos os números que obtiver: 2 + 400 + 10 + 5 = 417. Assim, 815-398-417.






