- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:13.
- Última modificação 2025-01-23 12:43.
A subtração é simplesmente subtrair um número de outro. É fácil subtrair um número inteiro de outro, mas a subtração pode ser complicada se você estiver subtraindo frações ou decimais. Depois de entender a subtração, você será capaz de usar conceitos matemáticos mais complexos e de somar, multiplicar e dividir números com mais facilidade.
Etapa
Método 1 de 6: subtraindo grandes números inteiros por empréstimo

Etapa 1. Escreva um grande número
Por exemplo, você deseja resolver 32 - 17. Escreva 32 primeiro.

Etapa 2. Escreva o número menor logo abaixo
Certifique-se de colocar os valores das dezenas e unidades nas colunas corretas, de forma que 3 de 32 esteja diretamente acima de 1 de 17 e 2 de 32 esteja diretamente acima de 7 de 17.
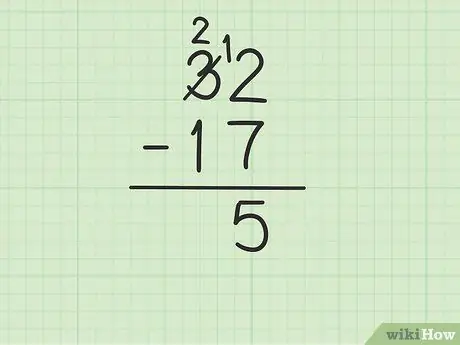
Etapa 3. Subtraia o número superior na coluna de unidades do número inferior
No entanto, isso pode ficar complicado se o número inferior for maior do que o número superior. Nesse caso, 7 é maior que 2. Aqui está o que você deve fazer:
- Você precisa pegar emprestado do número 3 de 32 (também conhecido como agrupamento) para transformar 2 em 12.
- Cruze o número 3 de 32 e substitua-o pelo número 2, enquanto o número 2 passa a ser 12.
- Agora você pode subtrair 12 - 7, que é igual a 5. Escreva 5 sob os dois números que você está subtraindo para que eles fiquem na coluna de unidades da nova linha.
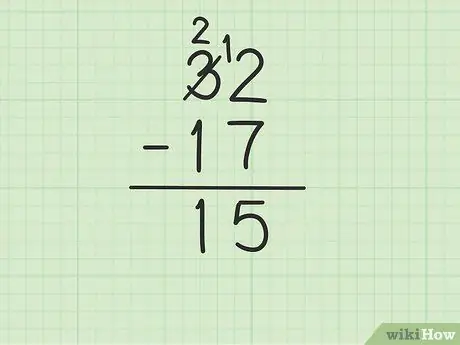
Etapa 4. Subtraia o número superior na coluna das dezenas do número inferior
Lembre-se de que 3 se tornou 2. Agora subtraia 1 de 17 de 2 acima para obter (2-1) 1. Escreva 1 abaixo, na coluna das dezenas, à esquerda de 5 na coluna das unidades. Você escreve 15. Ou seja, 32 - 17 = 15.
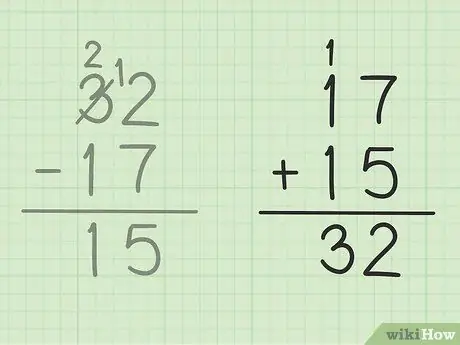
Etapa 5. Verifique seu trabalho
Se quiser ter certeza de que subtraiu dois números corretamente, tudo o que você precisa fazer é somar sua resposta com o número menor para formar um número grande. Neste problema, você tem que adicionar sua resposta, 15 ao menor número de subtração, 17. 15 + 17 = 32, para que sua resposta esteja correta. Seguro!
Método 2 de 6: subtraia números inteiros pequenos
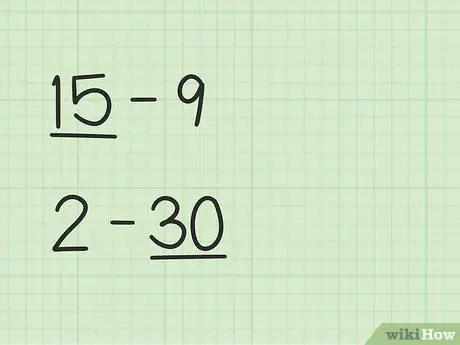
Etapa 1. Encontre o número maior
Problemas como 15 -9 terão uma maneira diferente de 2 - 30.
- Nas questões 15 - 9, o primeiro número, 15, é maior do que o segundo número, 9.
- Nas questões 2 - 30, o segundo número, 30, é maior do que o primeiro número, 2.
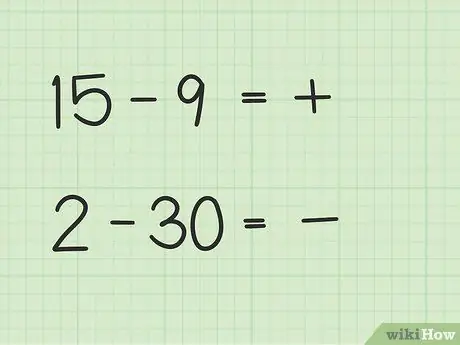
Etapa 2. Decida se sua resposta será positiva ou negativa
Se o primeiro número for maior, a resposta é positiva. Se o segundo número for maior, a resposta é negativa.
- Na primeira pergunta, 15 - 9, sua resposta é positiva porque o primeiro número é maior que o segundo.
- Na segunda pergunta, 2 - 30, sua resposta é negativa porque o segundo número é maior que o primeiro.
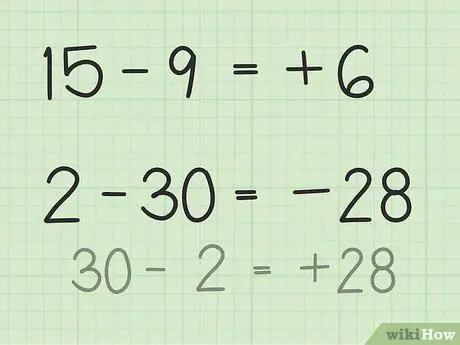
Etapa 3. Encontre a diferença entre dois números
Para subtrair dois números, você deve imaginar a diferença entre os dois números e calcular os números entre eles.
- Para as perguntas de 15 a 9, imagine uma pilha de 15 fichas de pôquer. Jogue fora 9 fichas e apenas 6. Portanto, 15 - 9 = 6. Você também pode imaginar uma reta numérica. Pense nos números de 1 a 15 e, em seguida, descarte ou devolva 9 unidades para obter 6.
- Para as questões 2 - 30, a maneira mais fácil de resolver isso é inverter o número e tornar o resultado negativo após a subtração. Portanto, 30 - 2 = 28, portanto, 28 e 30 têm uma diferença de 2. Agora, torne o resultado negativo porque você já determinou que a resposta é negativa porque o segundo número é maior que o primeiro. Portanto, 2 - 30 = -28.
Método 3 de 6: subtração de decimais
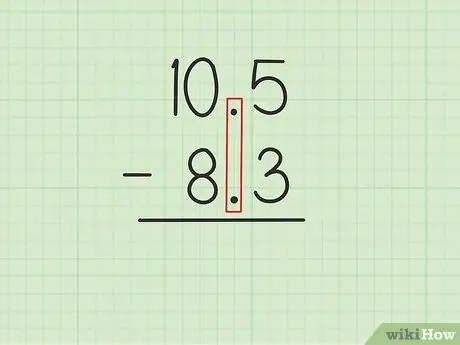
Etapa 1. Escreva o número maior sobre o número menor com as casas decimais alinhadas
Suponha que você queira resolver os seguintes problemas: 10, 5 - 8, 3. Escreva 10, 5 sobre 8, 3 de forma que as casas decimais dos dois números sejam paralelas., 5 de 10, 5 deve estar diretamente acima, 3 de 8, 3 e 0 de 10, 5 deve estar acima de 8 de 8, 3.
Se você tiver um problema porque os dois números não têm o mesmo número após a vírgula, escreva 0 no espaço em branco até que a soma dos números seja a mesma. Por exemplo, o problema é 5, 32 - 4, 2, você pode escrevê-lo como 5, 32 - 4, 2 0. Isso não mudará o valor do segundo número, mas tornará mais fácil subtrair os dois números.

Etapa 2. Subtraia o número superior na coluna das dezenas do número abaixo
Neste caso, você tem que subtrair 3 de 5. 5 - 3 = 2, então você tem que escrever 2 em 3 de 8, 3.
Certifique-se de colocar um ponto decimal na resposta, para que seja escrito, 2

Etapa 3. Subtraia o número acima da coluna de unidades do número abaixo dela
Você tem que subtrair 8 de 0. Pegue emprestado 1 da parte das dezenas para alterar 0 para 10 e subtraia 10 - 8 para obter 2. Você também pode contar 10 - 8 sem pedir emprestado porque não há números na segunda coluna das dezenas. Escreva a resposta em 8, à esquerda da vírgula decimal.

Etapa 4. Anote seu resultado final
Seu resultado final é 2, 2.

Etapa 5. Verifique seu trabalho
Se você quiser ter certeza de que sua subtração decimal está correta, tudo o que você precisa fazer é somar sua resposta com o número menor para formar o número maior. 2, 2 + 8, 3 = 10, 5, então você terminou.
Método 4 de 6: subtrair frações

Etapa 1. Alinhe o denominador e o numerador da fração
Suponha que você queira resolver os problemas 13/10 - 3/5. Escreva o problema de forma que os dois numeradores, 13 e 3, e os dois denominadores, 10 e 5, fiquem opostos. Esses dois números são separados por um sinal de subtração. Isso o ajudará a visualizar o problema e resolvê-lo com mais facilidade.

Etapa 2. Encontre o mínimo denominador comum
O mínimo denominador comum é o menor número que pode ser dividido por dois números. Neste exemplo, você precisa encontrar o menor denominador comum divisível por 10 e 5. Você descobrirá que 10 é o menor denominador comum para ambos os números porque 10 é divisível por 10 e 5.
Observe que o mínimo denominador comum de dois números nem sempre é um deles. Por exemplo, o menor denominador comum para 3 e 2 é 6 porque 6 é o menor número que pode ser dividido por dois números
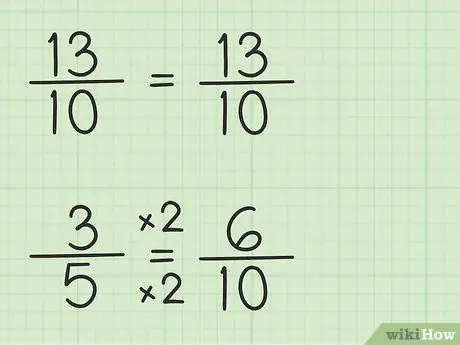
Etapa 3. Anote as frações usando o mesmo denominador
A fração 13/10 pode ser escrita da mesma maneira porque o denominador é 10, o menor denominador comum, que é 10 vezes 1. No entanto, a fração 3/5 deve ser reescrita porque o denominador é 5, o menor denominador comum, que é 10, vezes 2. Portanto, a fração 3/5 deve ser multiplicada por 2/2 para formar o denominador 10, então 3/5 x 2/2 = 6/10. Você encontrou a fração equivalente. 3/5 é equivalente a 6/10, embora 6/10 permita que você subtraia o primeiro número, 13/10.
Escreva uma nova pergunta como esta: 13/10 - 6/10
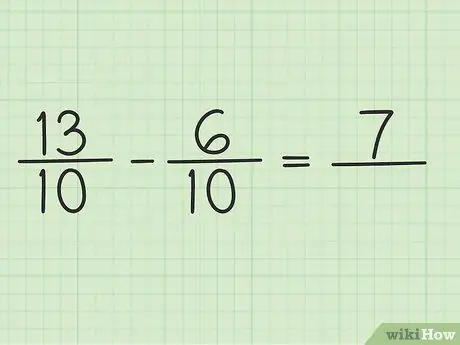
Etapa 4. Subtraia o numerador a dois números
Basta subtrair 13 - 6 para que o resultado seja 7. Você não pode alterar o denominador da fração.
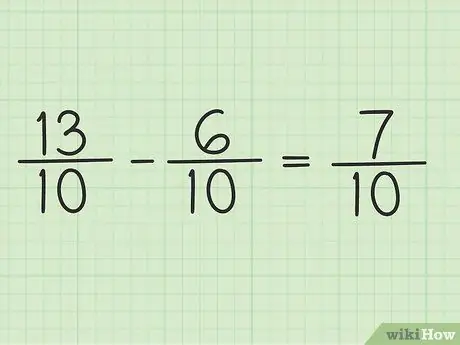
Etapa 5. Escreva o novo numerador sobre o mesmo denominador para obter o resultado final
O novo numerador é 7. Ambas as frações têm um denominador de 10. Seu resultado final é 7/10.
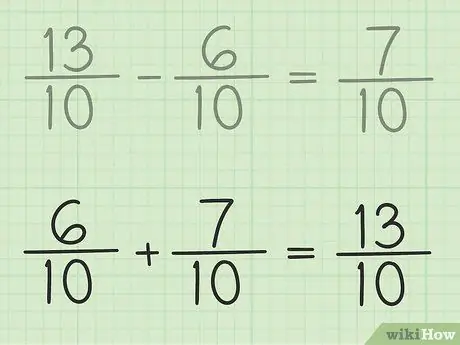
Etapa 6. Verifique seu trabalho
Se quiser ter certeza de que está subtraindo a fração corretamente, basta somar sua resposta e a fração menor para que o resultado seja uma fração maior. 7/10 + 6/10 = 13/10. Está pronto.
Método 5 de 6: subtraindo frações de números inteiros

Etapa 1. Anote o problema
Por exemplo, suponha que você queira resolver o seguinte problema: 5 -. Anotá-la.
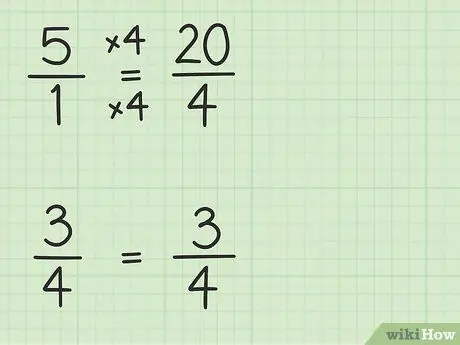
Etapa 2. Converta números inteiros em frações que tenham o mesmo denominador de outras frações
Você estará convertendo 5 em uma fração com um denominador de 4 para poder subtrair dois números. Portanto, você precisa pensar em 5 como uma fração de 5/1. Em seguida, você pode multiplicar o numerador e o denominador da nova fração por 4 para tornar os denominadores dos dois números iguais. Portanto, 5/1 x 4/4 = 20/4. Esta fração é igual a 5, mas permite que você subtraia dois números.
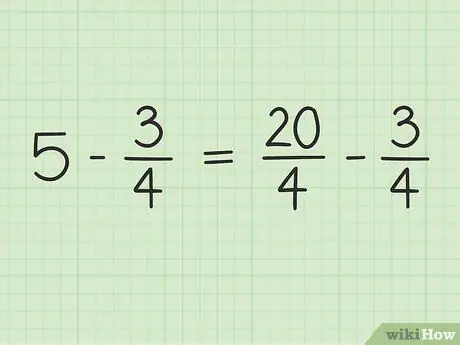
Etapa 3. Reescreva o problema
O novo problema pode ser escrito assim: 20/4 - 3/4.
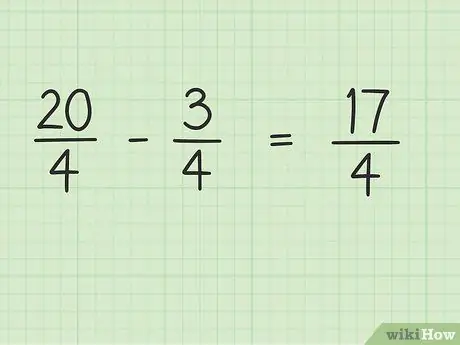
Etapa 4. Subtraia o numerador da fração, enquanto o denominador permanece o mesmo
Agora, basta subtrair 20 por 3 para obter o resultado final. 20 - 3 = 17, então 17 é o novo numerador. Você pode deixar o denominador igual.
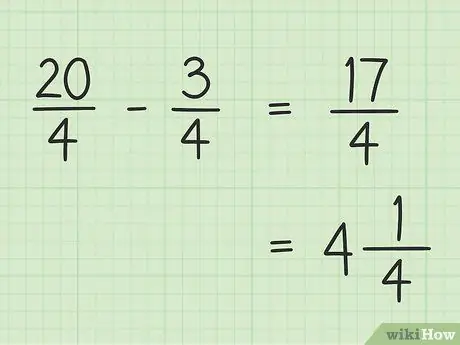
Etapa 5. Anote seu resultado final
Seu resultado final é 17/4. Se você quiser escrever como um número misto, divida 17 por 4 para que o resultado seja 4 e o resto seja 1, de modo que seu 17/4 final seja igual a 4.
Método 6 de 6: subtraindo variáveis
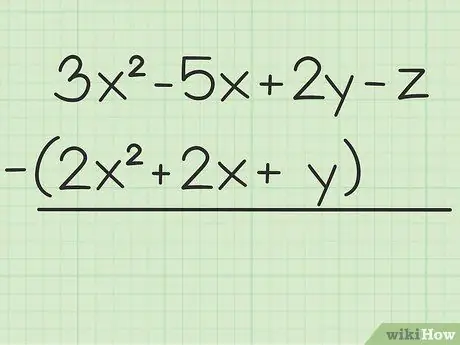
Etapa 1. Anote o problema que deseja resolver
Por exemplo, a seguinte pergunta: 3x2 - 5x + 2y - z - (2x2 + 2x + y). Escreva o primeiro conjunto de variáveis sobre o segundo.
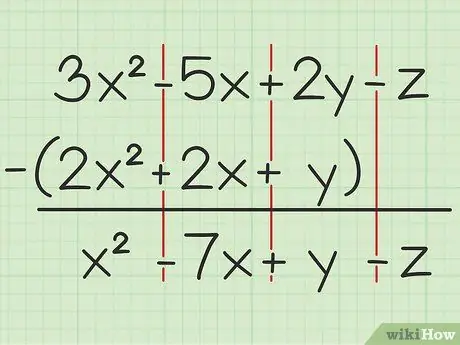
Etapa 2. Subtraia as mesmas variáveis
Se você encontrar uma variável, você só pode adicionar ou subtrair a mesma variável e que é escrita com o mesmo grau de quadrado. Isso significa que você pode subtrair 4x2 de 7x2, mas não pode subtrair 4x de 4y. Então, você pode dividir o problema assim:
- 3x2 - 2x2 = x2
- -5x - 2x = -7x
- 2y - y = y
- -z - 0 = -z
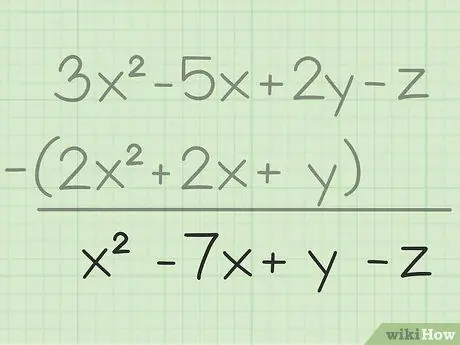
Etapa 3. Anote seu resultado final
Você subtraiu todas as mesmas variáveis, tudo o que você precisa fazer é escrever seu resultado final, que conterá todas as variáveis que você subtraiu. Aqui está o resultado final:






