- Autor Jason Gerald [email protected].
- Public 2024-01-19 22:13.
- Última modificação 2025-01-23 12:43.
A matemática é difícil. É fácil esquecer até mesmo os conceitos básicos quando você tenta se lembrar dos muitos princípios e métodos diferentes. Aqui estão duas novas maneiras de simplificar as frações.
Etapa
Método 1 de 4: usando o maior fator comum

Etapa 1. Anote os fatores do numerador e do denominador
Fatores são números que você pode multiplicar para obter outro número. Por exemplo, 3 e 4 são fatores de 12 porque você pode multiplicá-los para obter 12. Para escrever os fatores de um número, você só precisa anotar todos os números que podem ser multiplicados para obter esse número, e são divisíveis pelos fatores.
-
Anote os fatores do número do menor ao maior, sem se esquecer de incluir o fator 1. Por exemplo, aqui está como você escreve o numerador e o denominador da fração 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Etapa 2. Encontre o maior fator comum (GCF) do numerador e denominador
GCF é o maior número que pode dividir uniformemente dois ou mais números. Depois de anotar todos os fatores do número, tudo o que você precisa fazer é encontrar o maior número que seja o mesmo em ambas as listas de fatores.
-
24: 1, 2, 3, 4, 6,
Etapa 8., 12, 24.
-
32: 1, 2, 4,
Etapa 8., 16, 32.
-
O GCF de 24 e 32 é 8 porque 8 é o maior número que pode dividir igualmente 24 e 32.

Etapa 3. Divida o numerador e a fração pelo GCF
Agora que você tem o GCF, tudo o que você precisa fazer é dividir o numerador e o denominador por esse número para simplificar sua fração à sua forma mais simples. Veja como fazer:
- 24/8 = 3
- 32/8 = 4
- A fração simples é 3/4.

Etapa 4. Verifique seu trabalho
Se você quiser ter certeza de que simplificou a fração corretamente, você só precisa multiplicar o novo numerador e denominador por seu GCF para obter a fração original de volta. Veja como fazer:
- 3 * 8 = 24
- 4 * 8 = 32
-
Você voltou à forma original, que é 24/32.
Você também pode verificar a fração para garantir que não possa ser mais simplificada. Como 3 é um número primo, ele só pode ser dividido por 1 e ele mesmo, e quatro não é divisível por 3, portanto, a fração não pode ser mais simplificada
Método 2 de 4: continue dividindo por pequenos números

Etapa 1. Escolha um pequeno número
Usando este método, você só precisa escolher um pequeno número, como 2, 3, 4, 5 ou 7, para começar. Observe as frações para ter certeza de que cada parte é divisível pelo número que você escolheu. Por exemplo, se você tem uma fração 24/108, não escolha 5 porque eles não são divisíveis por 5. No entanto, se você tiver uma fração 25/60, 5 é o número certo a ser usado.
Para a fração 24/32, 2 é um bom número. Como os dois números são pares, eles são divisíveis por 2

Etapa 2. Divida o numerador e o denominador da fração pelo número
A nova fração consistirá em um novo numerador e denominador, que você obtém depois de dividir o topo e o fundo da fração 24/32 por 2. Veja como fazer isso:
- 24/2 = 12
- 32/2 = 16
- Sua nova fração é 12/16.
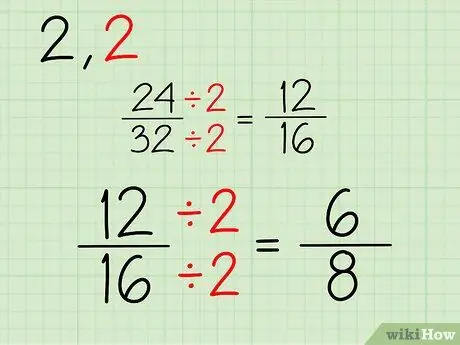
Etapa 3. Repita
Continue este processo. Como os dois números são pares, você pode continuar dividindo por 2. Se um ou ambos os numeradores e denominadores forem números ímpares, você pode tentar dividir por outro número. Este é o processo para simplificar a fração 12/16:
- 12/2 = 6
- 16/2 = 8
- Sua nova fração é 6/8.

Etapa 4. Continue dividindo o número até que ele não seja mais divisível
O novo numerador e denominador também são números pares, então você pode continuar dividindo por 2. Veja como fazer isso:
- 6/2 = 3
- 8/2 = 4
- Sua nova fração é 3/4.

Etapa 5. Certifique-se de que a fração não possa ser mais simplificada
Na fração 3/4, 3 é um número primo, então os fatores são apenas 1 e ele mesmo, e 4 não é divisível por 3, então a fração não pode ser mais simplificada. Se o numerador ou denominador da fração não puder mais ser dividido pelo número selecionado, você ainda poderá dividi-lo por outro número.
Por exemplo, se você tiver a fração 10/40 e dividir o numerador e o denominador por 5, o resultado será 2/8. Você não pode continuar dividindo o numerador e a fração por 5, mas pode dividir os dois por 2 para que o resultado final seja 1/4

Etapa 6. Verifique seu trabalho
Multiplique 3/4 por 2/2 novamente três vezes, para ter certeza de obter a fração inicial, que é 24/32. Veja como fazer:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Observe que você está dividindo 24/32 por 2 * 2 * 2, que é o mesmo que dividir por 8, o maior GCF de 24 e 32.
Método 3 de 4: Escrevendo os fatores

Etapa 1. Anote sua fração
Deixe um grande espaço no lado direito do papel - você precisará dele para anotar os fatores.

Etapa 2. Anote os fatores do numerador e denominador
Sozinhos os fatores dos dois. A maneira mais fácil é os fatores serem escritos uns sobre os outros. Comece com o número 1 e anote os fatores.
-
Por exemplo, se sua fração é 24/60, comece com 24.
Anote: 24 - 1, 2, 3, 4, 6, 8, 12, 24
-
Depois, o número 60.
Escreva: 60 - 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Etapa 3. Encontre e divida pelo maior fator comum
Este termo pode ser escrito como GCF em seu livro impresso. Qual é o maior número que pode dividir o numerador e o denominador? Seja qual for o número, divida os dois números por esse número.
Para nosso exemplo, o maior número que é um fator de ambos os números é 12. Assim, dividimos 24 por 12 e 60 por 12, nos dando 2/5 - nossa fração simples
Método 4 de 4: usando uma árvore de fatores primários

Etapa 1. Encontre os fatores principais do numerador e denominador
Um número primo é um número que não pode ser dividido por nenhum outro número (exceto ele mesmo e 1, é claro). 2, 3, 5, 7 e 11 são exemplos de números primos.
- Comece com o numerador. De 24, divida em 2 e 12. Como 2 já é um número primo, você não precisa mais dividi-lo! Em seguida, divida 12 em 2 números: 2 e 6. 2 são números primos - ótimo! Agora divida 6 em 2 números: 2 e 3. Você agora tem 2, 2, 2 e 3 como seus números primos.
- Agora trabalhe no denominador. De 60, divida sua árvore em 2 e 30. 30 e depois divida em 2 e 15. Em seguida, divida 15 em 3 e 5, ambos números primos. Agora você tem 2, 2, 3 e 5 como seus números primos.
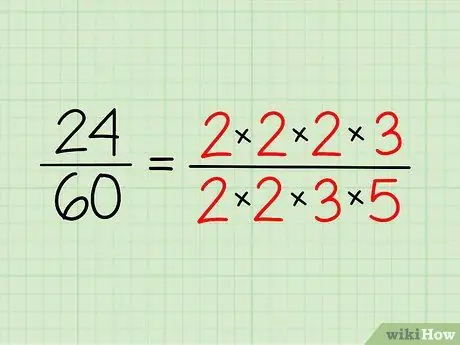
Etapa 2. Escreva a fatoração principal de cada número
Escreva os números primos que você tem para cada número e escreva-os em forma de multiplicação. Você não precisa multiplicar - é apenas uma maneira de tornar mais fácil de ver.
- Portanto, para 24, você tem 2 x 2 x 2 x 3 = 24.
- Para 60, você tem 2 x 2 x 3 x 5 = 60

Etapa 3. Elimine os mesmos fatores
Qualquer número que faça parte de ambos os números pode ser descartado. Neste exemplo, os fatores iguais são um par de 2s e um 3. Adeus!
- O resto são 2 e 5 - ou 2/5! A mesma resposta que obtivemos acima.
- Se o numerador e o denominador da fração forem números pares, não divida apenas por dois. Continue a fazer a divisão até que o número obtido não possa ser dividido novamente.






