- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:22.
- Última modificação 2025-01-23 12:43.
A gravidade é uma das forças fundamentais da física. O aspecto mais importante da gravidade é que ela é universal: todos os objetos têm uma força gravitacional que atrai outros objetos. A magnitude da força gravitacional depende da massa e da distância entre os dois objetos.
Etapa
Parte 1 de 2: Calculando a força da gravidade entre dois objetos

Etapa 1. Defina a equação para a força gravitacional puxando um objeto, Fgrav = (Gm1m2) / d2.
Para poder calcular a força gravitacional de um objeto, esta equação também leva em consideração as massas dos dois objetos e sua distância um do outro. As variáveis da equação são descritas a seguir.
- Fgrav é a força gravitacional
- G é a constante gravitacional universal 6,673 x 10-11 Nm2/kg2
- m1 é a massa do primeiro objeto
- m2 é a massa do segundo objeto
- d é a distância entre os centros dos dois objetos
- Às vezes, você encontra a letra r em vez de d. Esses dois símbolos representam a distância entre os dois objetos.

Etapa 2. Use as unidades métricas apropriadas
Para esta equação, você deve usar unidades métricas. A massa do objeto deve ser em quilogramas (kg) e a distância entre os objetos deve ser em metros (m). Você deve converter essas unidades em unidades métricas antes de prosseguir

Etapa 3. Determine a massa do objeto em questão
Para objetos pequenos, você pode pesá-los para determinar seu peso em quilogramas. Para objetos grandes, você pode consultar a massa aproximada em uma mesa ou na internet. Em problemas de física, geralmente a massa do objeto será informada.

Etapa 4. Meça a distância entre os dois objetos
Se você está tentando calcular a força gravitacional entre um objeto e a Terra, precisa saber a que distância esse objeto está do centro da Terra.
- A distância da superfície da Terra ao centro da Terra é de cerca de 6,38 x 106 m.
- Você pode procurar tabelas ou outras fontes na Internet que informam a distância aproximada do centro da Terra a objetos em várias alturas na superfície da Terra.

Etapa 5. Conclua o cálculo
Se você definiu as variáveis na equação, sinta-se à vontade para inseri-las para resolver. Certifique-se de que todas as variáveis estão em unidades métricas e dimensionadas corretamente. A massa deve ser em quilogramas e a distância deve ser em metros. Resolva as equações na ordem correta dos cálculos.
- Por exemplo, determine a força gravitacional de uma pessoa cuja massa é 68 kg acima da superfície da Terra. A massa da Terra é 5,98 x 1024 kg.
- Certifique-se de que todas as variáveis estão em unidades corretas. m1 = 5, 98 x 1024 kg, m2 = 68 kg, G = 6,673 x 10-11 Nm2/kg2, e d = 6, 38 x 106 m
- Escreva sua equação: Fgrav = (Gm1m2) / d2 = [(6, 67 x 10-11) x 68 x (5, 98 x 1024)] / (6, 38 x 106)2
- Multiplique as massas dos dois objetos que são levados em consideração. 68 x (5, 98 x 1024) = 4,06 x 1026
- Multiplique o resultado m1 e m2 com a constante gravitacional G. (4,06 x 1026) x (6,67 x 10-11) = 2.708 x 1016
- Quadrar a distância entre os dois objetos. (6, 38 x 106)2 = 4,07 x 1013
- Compartilhar resultado G x m1 x m2 pela distância ao quadrado para obter a força gravitacional em Newtons (N). 2, 708 x 1016/ 4, 07 x 1013 = 665 N
- Sua força gravitacional é de 665 N.
Parte 2 de 2: Calculando a Força da Gravidade na Terra

Etapa 1. Compreenda a Segunda Lei de Newton, F = ma
A segunda lei de Newton afirma que a aceleração de um objeto é diretamente proporcional à força resultante que atua sobre ele e inversamente proporcional à sua massa. Em outras palavras, se uma força atuando em um objeto for maior do que a força atuando na direção oposta, o objeto se moverá com a força mais forte.
- Essa lei pode ser resumida pela equação F = ma, onde F é a força, m é a massa do objeto e a é a aceleração.
- Graças a essa lei, podemos calcular a força gravitacional de todos os objetos na superfície da Terra, usando a aceleração conhecida da gravidade.
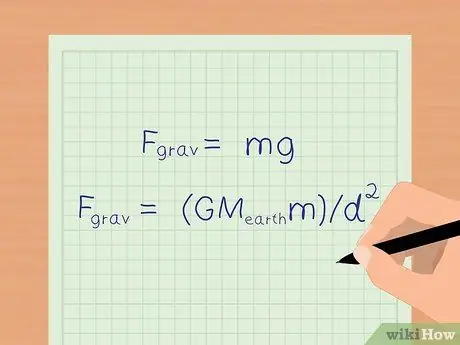
Etapa 2. Encontre a aceleração devido à gravidade da Terra
Na terra, a força da gravidade faz com que todos os objetos acelerem em 9,8 m / s2. Na superfície da Terra, podemos usar uma equação simplificada: Fgrav = mg para calcular a força gravitacional.
Se você quiser saber um número mais preciso de forças gravitacionais, você ainda pode usar a fórmula da etapa anterior, Fgrav = (GMterram) / d2 para determinar a força gravitacional.

Etapa 3. Use as unidades métricas apropriadas
Para esta equação, você deve usar unidades métricas. A massa do objeto deve ser em quilogramas (kg) e a distância entre os objetos deve ser em metros (m). Você deve converter essas unidades em unidades métricas antes de prosseguir.

Etapa 4. Determine a massa do objeto em questão
Para objetos pequenos, você pode pesá-los para determinar seu peso em quilogramas. Para objetos grandes, você pode consultar a massa aproximada em uma mesa ou na internet. Em problemas de física, geralmente a massa do objeto será informada.

Etapa 5. Conclua o cálculo
Se você definiu as variáveis na equação, sinta-se à vontade para inseri-las para resolver. Certifique-se de que todas as variáveis estão em unidades métricas e dimensionadas corretamente. A massa deve ser em quilogramas e a distância deve ser em metros. Resolva as equações na ordem correta dos cálculos.
- Vamos tentar usar a equação da etapa anterior e ver quão próximos estão os resultados. Determine a força gravitacional de uma pessoa com massa de 68 kg na superfície da Terra.
- Certifique-se de que todas as variáveis estão nas unidades corretas: m = 68 kg, g = 9,8 m / s2.
- Escreva a fórmula. Fgrav = mg = 68 * 9, 8 = 666 N.
- Usando a fórmula F = mg, a força gravitacional é 666 N, enquanto o resultado da fórmula da etapa anterior é 665 N. Como você pode ver, os dois resultados são quase os mesmos.
Pontas
- Essas duas fórmulas devem dar a mesma resposta, mas a fórmula mais curta e simples é mais fácil de usar ao discutir objetos na superfície de um planeta.
- Use a primeira fórmula se você não souber a aceleração da gravidade em um planeta ou se estiver calculando a força gravitacional entre dois objetos muito grandes, como a lua ou planetas.






