Como encontrar o número de termos em uma série aritmética: 3 etapas

Índice:

Como encontrar o número de termos em uma série aritmética: 3 etapas
Como encontrar o número de termos em uma série aritmética: 3 etapas

Vídeo: Como encontrar o número de termos em uma série aritmética: 3 etapas

Vídeo: Como encontrar o número de termos em uma série aritmética: 3 etapas
Vídeo: COMO CALCULAR A FREQUÊNCIA DE ONDAS - DICA ENEM #4 2024, Maio
Anonim

Encontrar o número de termos em uma série aritmética pode parecer assustador, mas na verdade é muito simples. Você só precisa inserir os números na fórmula U = a + (n - 1) be encontre o valor de n, que é o número de termos. Saiba que você é o último número da série, a é o primeiro termo da série e b é a diferença entre os termos adjacentes.

Etapa

Encontre um número de termos em uma sequência aritmética Etapa 1
Encontre um número de termos em uma sequência aritmética Etapa 1

Etapa 1. Identifique o primeiro, o segundo e o último termos da série

Normalmente, perguntas como esta fornecem os primeiros 3 ou mais termos e o último termo.

Por exemplo, suponha que sua pergunta seja assim: 107, 101, 95… -61. Nesse caso, o primeiro termo é 107 e o último termo é -61. Você precisa de todas essas informações para resolver o problema

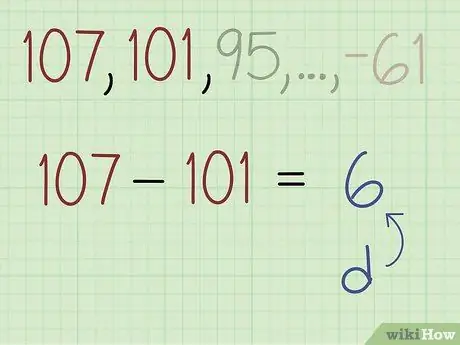
Encontre um número de termos em uma sequência aritmética Etapa 2
Encontre um número de termos em uma sequência aritmética Etapa 2

Etapa 2. Subtraia o segundo termo do primeiro termo para encontrar a diferença (b)

No problema de exemplo, o primeiro termo é 107 e o segundo termo é 101. Para encontrar a diferença, subtraia 101 por 107 e obtenha -6.

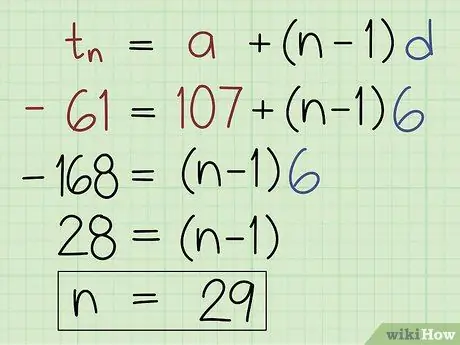
Encontre um número de termos em uma sequência aritmética Etapa 3
Encontre um número de termos em uma sequência aritmética Etapa 3

Etapa 3. Use a fórmula U = a + (n - 1) b para encontrar n.

Insira o último termo (U ), o primeiro termo (a) e a diferença (b). Conte as equações até obter o valor de n.

Para nosso problema de exemplo, escreva: -61 = 107 + (n - 1) -6. Subtraia 107 de ambos os lados de modo que apenas -168 = (n - 1) -6 permaneça. Em seguida, divida ambos os lados por -6 para obter 28 = n - 1. Resolva adicionando 1 a ambos os lados, de modo que n = 29

Pontas

A diferença entre o primeiro e o último termo sempre será divisível por diferença

Recomendado:

Como entender os termos no mundo dos estoques: 14 etapas (com imagens)

Como entender os termos no mundo dos estoques: 14 etapas (com imagens)

Se você está começando a se interessar por ações, provavelmente já decidiu por uma ou duas empresas para estudar. Em geral, qualquer empresa cujas ações possam ser negociadas pode ser investigada e analisada por meio de seus termos de ações.

Como compreender vários termos relacionados à identidade sexual

Como compreender vários termos relacionados à identidade sexual

Está tendo problemas para entender os termos relacionados ao LGBTQ? Em caso afirmativo, tente ler este artigo para entender a diferença entre cada termo! Etapa Etapa 1. Aprenda os termos Embora lésbica, bissexual, gay, transgênero e queer sejam os termos mais comumente usados, na verdade existem termos não binários e assexuados.

Como Encontrar a Soma de uma Série Aritmética: 10 Passos (com Imagens)

Como Encontrar a Soma de uma Série Aritmética: 10 Passos (com Imagens)

Uma série aritmética é uma série de números em que cada termo aumenta em um valor constante. Para somar os números em uma série aritmética, basta somar cada número. No entanto, quando o número de números na série é muito grande, esse método se torna impraticável.

Como descobrir o número de série do seu telefone sem desmontá-lo: 10 etapas

Como descobrir o número de série do seu telefone sem desmontá-lo: 10 etapas

Você pode encontrar o número de série da maioria dos telefones facilmente por meio de um código especial ou de um aplicativo de configurações. No entanto, esta etapa pode não funcionar para exibir o número de série em telefones mais antigos ou com recursos.

4 maneiras de encontrar termos em uma sequência aritmética

4 maneiras de encontrar termos em uma sequência aritmética

Uma série aritmética é uma série de números em que a diferença entre um número e o número próximo a ele é sempre a mesma. Por exemplo, a série de números pares 0, 2, 4, 6, 8 { displaystyle 0, 2, 4, 6, 8} … adalah deret aritmetika karena selisih satu angka dengan angka berikutnya selalu 2.