Contanto que você saiba a medida dos outros dois ângulos, é fácil encontrar o terceiro ângulo de um triângulo. Você só precisa subtrair a soma dos dois ângulos em 180 graus. No entanto, também existem outras maneiras que você pode usar para encontrar o terceiro ângulo de um triângulo se a forma do problema for um pouco diferente do normal. Se você quiser saber como encontrar o terceiro ângulo de um triângulo, siga o guia abaixo.
Etapa
Método 1 de 3: usando as medidas dos outros dois ângulos
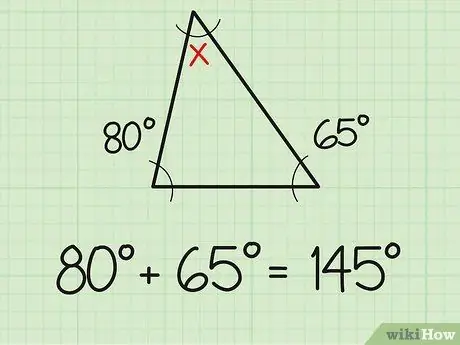
Etapa 1. Some os dois ângulos conhecidos
Um fato que você deve saber é que a soma dos três ângulos de um triângulo é sempre 180 graus. Portanto, se você já conhece a medida dos dois ângulos de um triângulo, encontrar o terceiro ângulo será tão simples quanto resolver problemas simples de adição e subtração. Primeiro, some as duas medidas angulares que você já conhece. Por exemplo, dois ângulos conhecidos medem 80 e 65 graus. Some os dois (80 + 65) e você terá 145 graus.
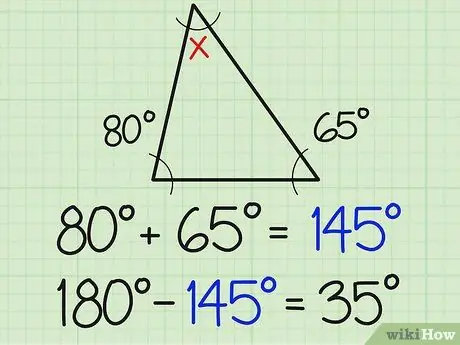
Etapa 2. Divida esse número por 180
A soma dos três ângulos de um triângulo é sempre 180 graus. Portanto, o terceiro ângulo deve ser 180 quando adicionado à soma das duas medidas conhecidas do ângulo. No exemplo acima, isso significa 180-154 = 35.
Etapa 3. Escreva sua resposta
Agora você tem a resposta para o terceiro ângulo (no exemplo, 35 graus). Se você ainda estiver em dúvida, veja por si mesmo. Some os três ângulos e você deve obter um resultado de 180. Do contrário, seu cálculo está errado. Para este exemplo, 80 + 65 + 35 = 180. Se estiver correto, significa que você resolveu o problema.
Método 2 de 3: usando variáveis
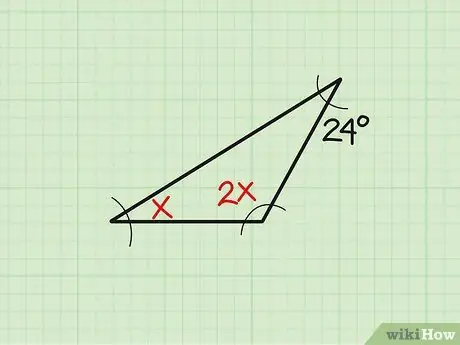
Etapa 1. Anote o problema
Às vezes, o tamanho do ângulo existente é mostrado em uma forma variável. Vejamos este exemplo: “Encontre o ângulo“x”de um triângulo se os três ângulos medem“x”,“2x”e 24, respectivamente.” Primeiro, escreva o problema.
Etapa 2. Some todas as medidas dos ângulos
O princípio que você deve lembrar permanece o mesmo. Portanto, primeiro some os três ângulos do problema, a saber "x + 2x + 24 = 3x + 24".
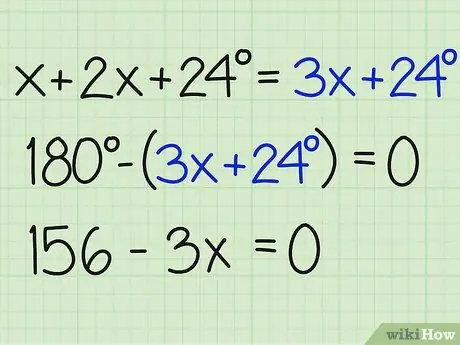
Etapa 3. Divida a soma dos ângulos por 180
Agora, diferencie esse número em 180 graus para encontrar xe descobrir a resposta para o problema. Certifique-se de terminar a equação igual a zero. Veja como está escrito:
- 180- (3x + 24) = 0
- 180-3x-24 = 0
- 156-3x = 0
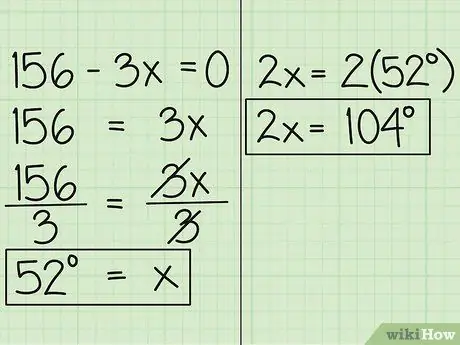
Etapa 4. Encontre o valor de x
Agora, mova a variável para o outro lado da equação e você obterá 156 = 3x. Em seguida, divida a equação por 3, para obter x = 52. Isso significa que a medida do ângulo expresso em x é de 52 graus. O outro ângulo, expresso em 2x, é 52 graus vezes 2, que é 104 graus.
Etapa 5. Verifique seus resultados
Se quiser ter certeza de que sua resposta está correta, basta somar as três medidas angulares para as quais você já encontrou a resposta. Se o resultado for 180, significa que sua resposta está correta. Para este exemplo, 52 + 104 + 24 = 180.
Método 3 de 3: usando outros métodos
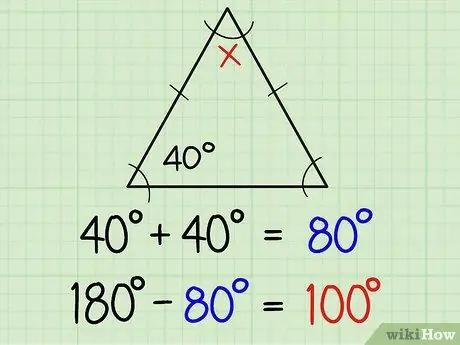
Etapa 1. Encontre os ângulos de um triângulo isósceles
Um triângulo isósceles tem dois lados iguais e dois ângulos iguais. Dois lados iguais são geralmente marcados com uma pequena linha no meio da linha lateral, o que significa que os dois ângulos opostos na linha têm a mesma medida. Se você já sabe o tamanho de um ângulo, conhece automaticamente o outro ângulo. Aqui está uma explicação adicional:
Se um dos ângulos iguais for de 40 graus, o outro será de 40 graus. Dessa forma, você pode encontrar todos os três ângulos com a diferença entre a soma de 40 + 40 (ou seja, 80) e 180 ou, em outras palavras, 180-80 = 100
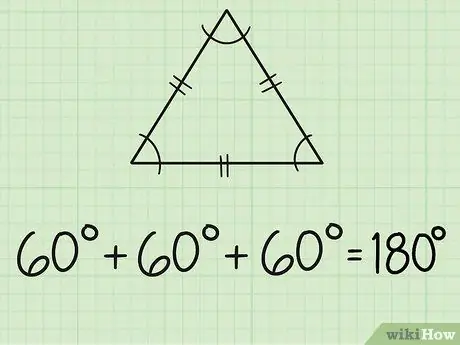
Etapa 2. Encontre os ângulos de um triângulo equilátero
Um triângulo equilátero tem três lados iguais e três ângulos iguais. Cada lado é geralmente marcado com duas linhas curtas no meio. Como todos os três ângulos são iguais, isso significa que todos os ângulos medem 60 graus, porque 180/3 = 60.
Etapa 3. Encontre o terceiro ângulo em um triângulo retângulo
Suponha que você obtenha um triângulo retângulo, com um dos ângulos agudos medindo 30 graus. Como o triângulo é um ângulo reto, significa que um dos ângulos, ou seja, o ângulo reto, deve medir 90 graus. Em seguida, use o princípio do triângulo, a diferença entre a soma dos dois ângulos (90 + 30 = 120) por 180, então você obterá 180-120 = 60 graus.
