- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:22.
- Última modificação 2025-01-23 12:43.
Você pode pensar que os inteiros são apenas números comuns, como 3, -12, 17, 0, 7000 ou -582. Os inteiros também são chamados de números inteiros porque não são divididos em partes como frações e decimais. Leia este artigo para aprender tudo o que você precisa sobre como adicionar e subtrair números inteiros ou leia diretamente a seção necessária.
Etapa
Método 1 de 5: adição e subtração de inteiros positivos usando uma linha numérica

Etapa 1. Compreenda sobre a reta numérica
As linhas numéricas transformam a matemática básica em algo tangível e físico que você pode ver. Com apenas alguns sinais e bom senso, podemos usá-lo como uma calculadora para somar e subtrair números.

Etapa 2. Desenhe uma linha de número base
Imagine ou desenhe uma linha reta uniforme. Faça um ponto no meio da linha. Escrever 0 ou zero próximo a este período.
Seu livro de matemática pode chamar isso de ponto de partida porque é o ponto de partida para todos os números

Etapa 3. Desenhe dois pontos, um à direita e outro à esquerda do seu zero
Escrever - 1 ao lado do ponto à esquerda e
Passo 1. ao lado do ponto à direita. Este é o número inteiro mais próximo de zero.
- Não se preocupe em tornar as distâncias entre os pontos exatamente iguais - contanto que você saiba o que cada ponto significa, uma reta numérica pode ser usada.
- O lado esquerdo é o início da frase.

Etapa 4. Complete sua linha numérica adicionando mais números
Faça mais pontos à esquerda do que -1 e à direita do que 1. À esquerda, de -1, marque seus pontos com - 2, - 3, e - 4. À direita, a partir de 1, marque o seu ponto com
Passo 2
Etapa 3., da
Passo 4.. Você pode continuar se tiver espaço em seu papel.
O exemplo na figura mostra uma reta numérica de -6 a 6

Etapa 5. Compreenda sobre inteiros positivos e negativos
Inteiros positivos, também chamados de número natural, é um número inteiro maior que zero. 1, 2, 3, 25, 99 e 2007 são números inteiros positivos. Inteiros negativos são inteiros menores que zero (como -2, -4 e -88).
Os inteiros são outra forma de chamar números inteiros. Frações como 1/2 (metade) são apenas parte do número, portanto, não são inteiros. O mesmo que decimal, por exemplo 0,25 (zero vírgula dois cinco); decimal não é um número inteiro

Etapa 6. Comece a resolver 1 + 2 colocando seu dedo no ponto 1
Vamos resolver problemas simples de adição 1+2 usando a linha numérica que você acabou de criar. O primeiro numero é
Passo 1., comece a colocar o dedo no número.
-
Esta pergunta é muito fácil?
Se você já adicionou, provavelmente sabe a resposta para 1 + 2. Bom: se você souber o resultado, será mais fácil entender como funciona a reta numérica. Em seguida, você pode usar a reta numérica para resolver problemas de adição mais difíceis ou se preparar para matemática mais difícil, como álgebra.

Etapa 7. Some 1 + 2 movendo o dedo 2 pontos para a direita
Deslize o dedo para a direita, contando o número de pontos (outro número) que você passa. Se você passou 2 novos pontos, pare. O número para o qual seu dedo está apontando é a resposta,
Etapa 3
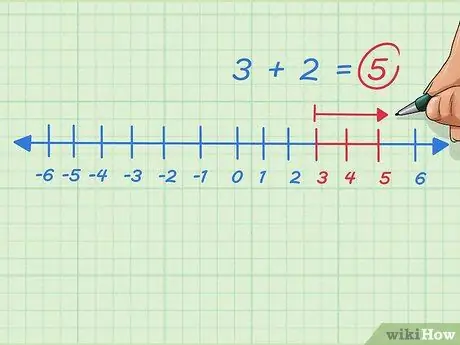
Etapa 8. Adicione quaisquer inteiros positivos movendo-se para a direita na reta numérica
Suponha que queremos resolver 3 + 2. Comece em 3, mova para a direita ou adicione 2 pontos. Paramos em 5. O problema está escrito 3 + 2 = 5.

Etapa 9. Subtraia os inteiros positivos movendo para a esquerda na reta numérica
Por exemplo, queremos resolver 6 -4, começamos em 6, movemos 4 pontos para a esquerda e paramos em 2. Este problema está escrito 6 - 4 = 2.
Método 2 de 5: adição e subtração de números negativos usando uma linha numérica

Etapa 1. Aprenda sobre as linhas numéricas
Se você não sabe como criar uma reta numérica, volte para a seção Adicionando e subtraindo números positivos usando linhas numéricas para aprender como criar uma.
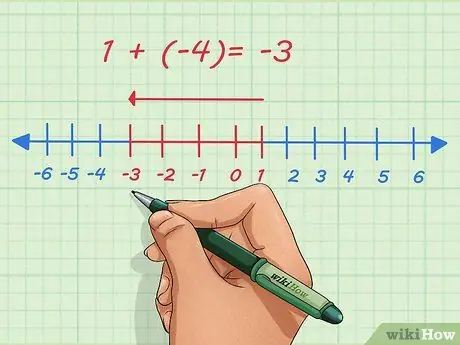
Etapa 2. Compreenda sobre os números negativos
Os números positivos são indicados pela direção à direita na linha do número. Os números negativos são indicados à esquerda na linha numérica. Adicionar números negativos significa mover o ponto para a esquerda na reta numérica.
-
Por exemplo, vamos adicionar 1 e -4. Normalmente, esta pergunta é escrita assim:
1 + (-4)
. Na reta numérica, começamos em 1, movemos 4 pontos para a esquerda e paramos em -3.
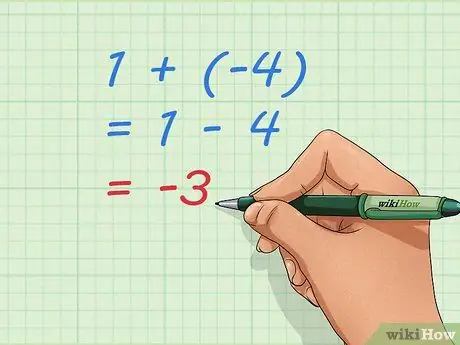
Etapa 3. Use equações básicas para entender a adição de números negativos
Observe que -3, nossa resposta, é o número que obteremos se fizermos 1 - 4. Adicionar 1 + (-4) e subtrair 4 de 1 é o mesmo problema. Podemos escrever como uma equação, uma frase matemática que mostra igualdade: 1 + (-4) = 1 - 4 = -3
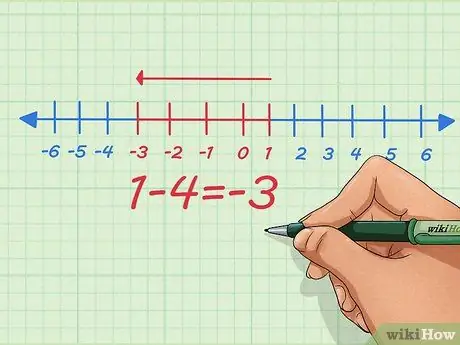
Etapa 4. Em vez de adicionar números negativos, transforme-o em um problema de subtração usando números positivos
Como podemos ver na equação simples acima, podemos fazer as duas coisas - transformar a adição de números negativos em subtração de números positivos e vice-versa. Você pode ter sido ensinado a transformar negativos em negativos sem saber por quê - aqui está o porquê.
-
Por exemplo, -4. Quando adicionamos -4 e 1, subtraímos 1 por 4. Pode ser escrito em matemática
1 + (-4) = 1 - 4
. Podemos escrever isso na reta numérica, começando em nosso ponto inicial em 1 e, em seguida, adicionando 4 pontos à esquerda (em outras palavras, adicionando -4). Uma vez que esta é uma equação, uma coisa é igual a outra - então o oposto também é verdadeiro
1 - 4 = 1 + (-4)
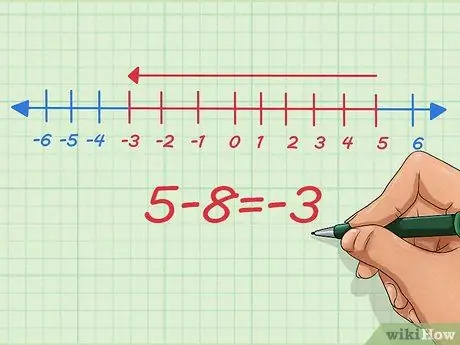
Etapa 5. Entenda como subtrair números negativos em uma reta numérica
Na reta numérica, subtrair números negativos é o mesmo que reduzir o comprimento. Vamos começar com 5 - 8.
Na reta numérica, começamos em nosso ponto inicial em 5, subtraímos 8 e paramos em -3
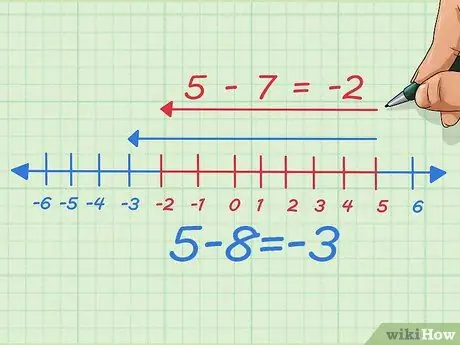
Passo 6. Subtraia a quantia que você está subtraindo e veja o que acontece
Suponha que subtraímos um, o número que subtraímos, ou em outras palavras, subtraímos 7 em vez de 8. Agora subtraímos um ponto à esquerda da reta numérica. Por escrito, começamos com 5 - 8 = -3 Agora, apenas movemos 7 para a esquerda, então ele se torna 5 - 7 = -2
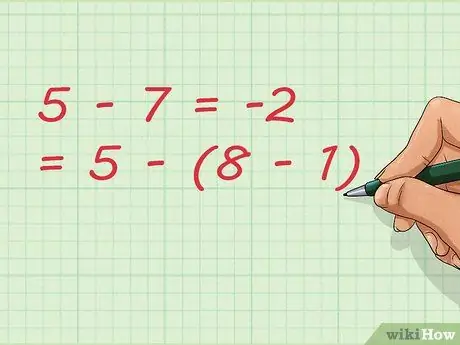
Etapa 7. Observe que a subtração pode resultar em adição
Em nosso exemplo, estamos subtraindo o número 1. Ao escrever a equação, podemos escrevê-la mais curta como: 5 - 7 = -2 = 5 - (8 - 1)

Etapa 8. Converta sinais negativos em positivos ao adicionar números negativos
Usando a etapa de conversão de todas as subtrações em adições, podemos escrever outras mais curtas, como: 5 - (8 - 1) = 5 - 7 = 5 - 8 + 1.
-
Já sabemos que 5 - 8 = -3, então tire 5 - 8 da equação e insira -3:
5 - (8 - 1) = 5 - 7 = -3 + 1
-
Já sabemos que 5 - (8 - 1) é - subtrai um ponto de 5 - 8. Nossa equação pode mostrar que 5 - 8 é igual a -3, e subtrair um ponto resulta em -2. A equação pode ser escrita assim:
-3 - (-1) = -3 + 1
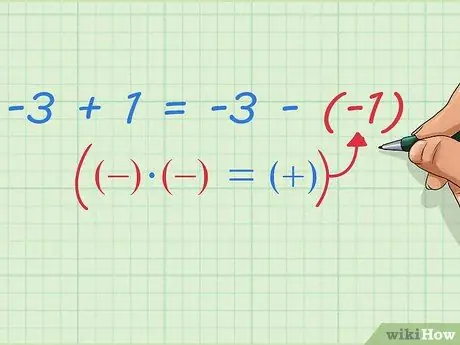
Etapa 9. Escreva a subtração de números negativos como adição
Observe o que acontece depois disso - já provamos que: -3 + 1 = -3 - (-1) Podemos escrever isso com regras de escrita matemática mais simples e gerais: primeiro número mais o segundo número = primeiro número menos (segundo número negativo) Ou uma maneira mais simples que você provavelmente já ouviu na aula de matemática: Mude os dois sinais negativos para um sinal positivo.
Método 3 de 5: adição de números inteiros grandes positivos

Etapa 1. Escreva o problema de adição de 2.503 + 7.461 com um número sobre o outro
Escreva os números na coluna grande de forma que 2 seja maior que 7, 5 seja maior que 4 e assim por diante. Desta forma, aprenderemos como adicionar inteiros que são muito grandes para imaginar ou usar a reta numérica.
Escreva um sinal de + à esquerda do número abaixo e na linha abaixo dele, como você pode aprender para problemas de adição menores
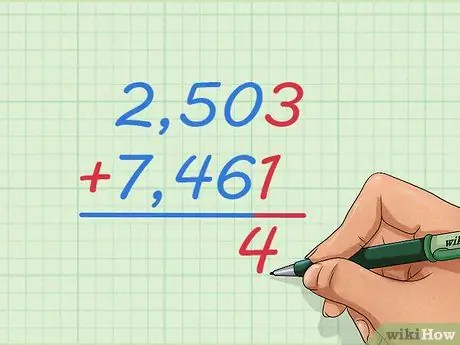
Etapa 2. Comece somando os dois números da extrema direita
Pode ser um pouco estranho começar da direita porque lemos os números da esquerda. Temos que adicionar da direita para obter a resposta correta, que você pode ver mais tarde.
-
Abaixo dos dois números mais à direita,
Etapa 3. da
Passo 1., escreva a soma dos dois
Passo 4..

Etapa 3. Some cada número na coluna da mesma maneira
Mova para a esquerda, some 0+6, 5+4, e 2+7. Escreva a resposta em cada par de números.
Sua resposta deve ser: 9.964. Verifique seu trabalho se cometer um erro.

Etapa 4. Agora some 857 + 135
Você notará algo diferente assim que somar o primeiro par de números à direita. 7+5 é igual a 12, um número de dois dígitos, mas você só pode escrever um dígito nessa coluna. Continue lendo para descobrir o que você deve fazer e por que você deve sempre começar da direita e não da esquerda.

Etapa 5. Some 7 + 5 e aprenda onde escrever a resposta
7 + 5 = 12, mas você não pode colocar 1 e 2 abaixo da linha. Mas, anote o último dígito, Passo 2., sob a linha e anote o primeiro dígito
Passo 1., acima da coluna à esquerda, 5 + 3.
-
Se você está curioso para saber como funciona, pense no que significa a divisão 1 e 2. Na verdade, você está dividindo 12 em
Etapa 10. da
Passo 2.. Você pode escrever 10 acima do número, se quiser, e verá 1 nas colunas 5 e 3, exatamente como antes.

Etapa 6. Some 1 + 5 + 3 para obter o próximo dígito da resposta
Agora você tem três dígitos para somar porque adicionou 1 a esta coluna. A resposta é
Etapa 9., então sua resposta se torna 92.
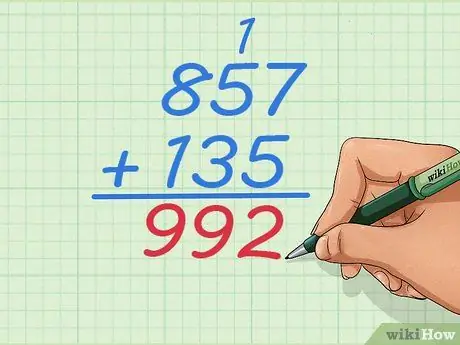
Etapa 7. Conclua o problema normalmente
Continue trabalhando os dígitos à esquerda até que você tenha somado todos os números, neste caso, há apenas uma coluna restante. Sua resposta final deve ser 992.
- Você pode tentar perguntas mais complicadas, como 974 + 568. Lembre-se, sempre que você obtiver um número de dois dígitos, escreva apenas o último dígito como a resposta e coloque o outro dígito acima da coluna à esquerda, que você adicionará em seguida. Se a resposta na última coluna (extrema esquerda) contiver dois dígitos, escreva-a como sua resposta.
- Consulte a seção Dicas para obter as respostas às perguntas 974 + 568 depois de tentar resolvê-las.
Método 4 de 5: Subtraindo números inteiros grandes positivos

Etapa 1. Escreva o problema de subtração 4,713 - 502 com o primeiro número acima do segundo número
Escreva de forma que 3 esteja diretamente acima de 2, 1 esteja acima de 0, 7 esteja acima de 5 e 4 esteja acima do espaço em branco.
Você pode escrever de 0 a 4 se isso ajudar a lembrar qual número está acima de qual número. Você sempre pode adicionar um 0 na frente de um número sem alterá-lo. Certifique-se de adicioná-lo antes do número, não depois dele

Etapa 2. Subtraia cada número abaixo do número diretamente acima dele
Sempre comece da direita. Resolva 3-2, 1-0, 7-5 e 4-0, escreva a resposta para cada pergunta diretamente abaixo dos dois números subtraídos.
O resultado é, 4.211.

Etapa 3. Agora, escreva as questões 924 - 518 da mesma maneira
Esses números têm o mesmo número de dígitos, então você pode anotá-los facilmente. Este problema vai te ensinar algo sobre como subtrair inteiros, se você ainda não souber.

Etapa 4. Aprenda como resolver o primeiro problema, que está à direita
4 - 8. Este problema é complicado porque 4 é menor que 8, mas não use números negativos, mas siga estas etapas:
- Na linha superior, cruze 2 e escreva 1. 2 deve estar à esquerda de 4.
- Cruze 4 e escreva 14. Faça isso em um espaço estreito para que fique claro que 14 é mais de 8. Você também pode escrever 1 na frente de 4 para fazer 14 se houver espaço suficiente.
- O que você acabou de fazer é pegar emprestado 1 na casa das dezenas ou a segunda coluna da direita e convertê-lo em 10 na casa das unidades ou na coluna da extrema direita. Uma vez que o número 10 é igual a dez vezes o número 1, então é o mesmo.

Etapa 5. Agora resolva os problemas 14-8 e escreva a resposta na coluna mais à direita
Deveria ter escrito 6 na linha de resposta mais à direita.

Etapa 6. Complete a próxima coluna à esquerda, usando o novo número que você anotou
A subtração deve ser 1 - 1, que é igual a 0.
Sua resposta agora deve ser 06.

Etapa 7. Resolva o problema completando a última subtração, a coluna mais à esquerda
9 - 5 = 4, então sua resposta final é 406.

Etapa 8. Agora resolvemos o problema de subtrair números grandes de números pequenos
Suponha que você seja solicitado a preencher 415.990 - 968.772. Escreva o segundo número abaixo do primeiro e você perceberá que o número abaixo é maior! Você pode dizer imediatamente pelo primeiro dígito à esquerda: 9 é maior do que 4, portanto, os números que começam com 9 são maiores.
Certifique-se de escrever a coluna corretamente antes de comparar. 912 não maior que 5000 você pode dizer se você escreveu a coluna corretamente porque não há números abaixo de 5. Você pode adicionar ajuda zero, por exemplo, escreva 912 com 0912 para que a coluna seja igual a 5000.

Etapa 9. Escreva o menor número sob o maior e adicione um sinal - antes da resposta
Sempre que você subtrai um número de um número menor, o resultado é um número negativo. É melhor escrever este sinal antes de subtrair, para não se esquecer de anotá-lo.

Etapa 10. Para responder, subtraia o número pequeno do número grande e lembre-se de escrever o sinal -
Sua resposta será negativa, o que é indicado por um sinal -. Não tenta subtrair um grande número de um pequeno número, então torna o resultado negativo; sua resposta estará errada.
O novo problema a resolver é: 968.772 - 415.990 = -? Consulte a seção Dicas para obter a resposta depois de tentar resolver esse problema
Método 5 de 5: adição e subtração de números inteiros negativos
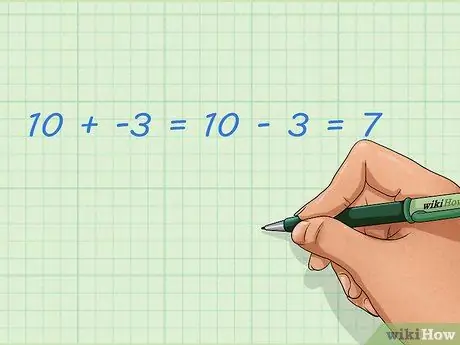
Etapa 1. Aprenda a somar números negativos e positivos
Adicionar números inteiros negativos é o mesmo que subtrair números inteiros positivos. Isso é mais fácil de fazer com a reta numérica descrita em outra seção, mas você também pode pensar nela em palavras. Números negativos não são números comuns; este número é menor que zero e pode representar a quantia tomada. Se você adicionar este take a um número normal, o resultado ficará menor.
- Exemplo: 10 + -3 = 10 - 3 = 7
- Exemplo: -12 + 18 = 18 + -12 = 18 - 12 = 6. Lembre-se de que você sempre pode alterar a ordem dos números na adição, mas não na subtração.
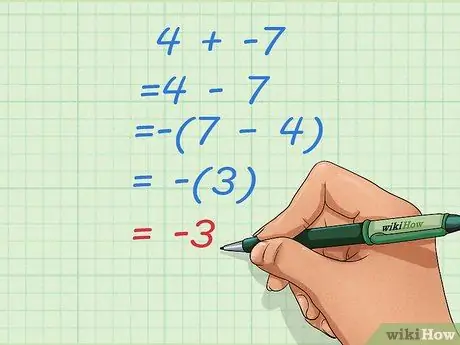
Etapa 2. Aprenda o que você deve fazer se transformar isso em um problema de subtração com um número inicial menor
Às vezes, alterar problemas de adição para subtração como o acima pode levar a respostas ímpares, como 4 - 7. Quando isso acontecer, inverta a ordem dos números e torne o resultado negativo.
- Digamos que seu problema inicial seja 4 + -7.
- Transforme isso em um problema de subtração: 4 - 7
- Inverta a ordem e torne o resultado negativo: - (7 - 4) = - (3) = -3.
- Se você não estiver familiarizado com o uso de colchetes em equações, pense no seguinte: 4 - 7 se transforma em 7 - 4 com a adição de um sinal negativo. 7 - 4 = 3, mas temos que alterá-lo para -3 para que a resposta às perguntas 4 - 7 esteja correta.
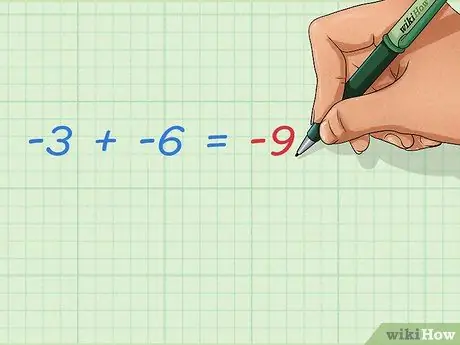
Etapa 3. Aprenda a adicionar dois inteiros negativos
Dois números negativos adicionados sempre tornam o resultado negativo maior. Como nenhum número positivo é adicionado, o resultado estará mais longe de 0. A resposta é fácil:
- -3 + -6 = -9
- -15 + -5 = -20
- Você vê o padrão? Tudo que você precisa fazer é somar os números como se fossem números positivos e adicionar um sinal negativo. -4 + -3 = - (4 + 3) = -7
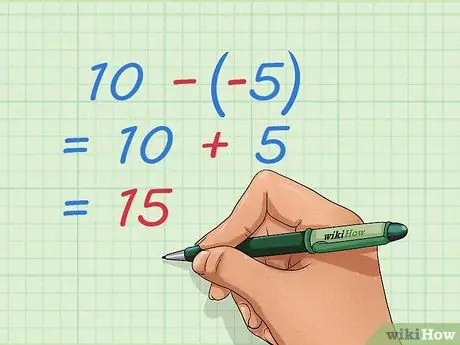
Etapa 4. Aprenda a subtrair inteiros negativos
Como no problema da adição, você pode reescrever o problema de forma que tenha apenas números positivos. Se você subtrair números negativos, tira algumas das coisas que já foram tiradas, o que é o mesmo que adicionar números positivos.
- Pense em números negativos como dinheiro roubado. Se você subtrair ou tirar dinheiro roubado para devolver, é como dar dinheiro para alguém, certo?
- Exemplo: 10 - -5 = 10 + 5 = 15
- Exemplo: -1 - -2 = -1 + 2. Você já aprendeu como resolver esse problema na primeira etapa, lembra? Releia como somar números negativos e positivos se você se esqueceu.
- Aqui está a solução completa do último exemplo: -1 - -2 = -1 + 2 = 2 + -1 = 2 - 1 = 1.
Pontas
- Você pode ter escrito números longos, como 2.521.301, usando vírgulas (,) em vez de (.), Dependendo de onde você mora. Use o que seu professor pedir para não se confundir com outros sistemas de escrita.
- Desenhe suas linhas numéricas em escalas diferentes para representar números diferentes. Não há regra segundo a qual toda distância em uma reta numérica seja igual a 1. Imagine uma reta numérica que é 10 em vez de 1. Além do fato de que cada ponto agora é 10, a adição e a subtração permanecem as mesmas. Experimente se você não acredita.
- Se você tentar as perguntas de desafio especiais na seção Números longos, aqui está a resposta: 974 + 568 = 1.542. A resposta de 415.990 a 968.772 é - 552.782.






