- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-02-01 14:15.
- Última modificação 2025-01-23 12:43.
O deslocamento na física denota uma mudança na posição de um objeto. Ao calcular o deslocamento, você calcula a distância de um objeto com base em suas localizações inicial e final. A fórmula que você usa para calcular o deslocamento depende da variável fornecida ao problema. Siga estas etapas para calcular o deslocamento.
Etapa
Parte 1 de 5: Calculando o deslocamento resultante

Etapa 1. Use a fórmula de deslocamento resultante se a unidade de distância for usada para indicar seus locais de partida e chegada
Embora a distância seja diferente do deslocamento, o problema de deslocamento resultante procura quantos quilômetros ou metros o objeto viajou. Você usará esta unidade de medida para calcular o deslocamento e quão longe a localização de um objeto se desvia de seu ponto inicial.
- A fórmula de deslocamento resultante é escrita como: S = x² + y². S é o deslocamento. X é a primeira direção de movimento do objeto e Y é a segunda direção de movimento do objeto. Se o seu objeto se move apenas em uma direção, então Y = 0.
- Um objeto só pode se mover em no máximo duas direções porque se mover ao longo de um eixo norte / sul ou leste / oeste é considerado um movimento neutro.

Etapa 2. Conecte os pontos em ordem de movimento e rotule-os de A-Z
Use uma régua para desenhar uma linha reta ponto a ponto.
- Lembre-se também de conectar seu ponto de partida ao ponto de chegada usando uma linha reta. Este é o deslocamento que calcularemos.
- Por exemplo, se um objeto se mover para o leste 300 m e para o norte 400 m, ele formará um triângulo retângulo. AB será a primeira etapa do triângulo e BC será a segunda etapa. AC será a hipotenusa do triângulo e sua magnitude é o deslocamento do objeto. Neste exemplo, as duas direções são leste e norte.

Etapa 3. Insira os valores para x² e y²
Agora que você conhece as duas direções de movimento do seu objeto, insira os valores nas variáveis apropriadas.
Por exemplo, x = 300 ey = 400. Sua fórmula deve ser assim: S = 300² + 400²
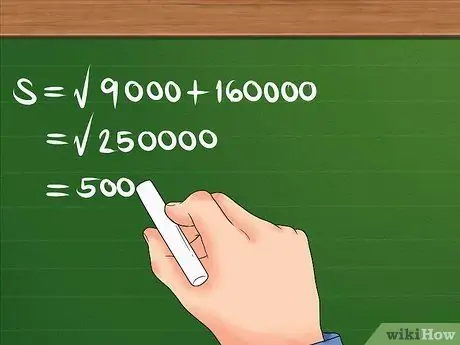
Etapa 4. Calcule a fórmula usando a ordem das operações
Quadrado 300 e 400 primeiro, depois some-os e encontre a raiz quadrada da soma.
Por exemplo: S = 90000 + 160000. S = 250000. S = 500. Agora você sabe que o deslocamento é de 500 m
Parte 2 de 5: Quando a velocidade e o tempo são conhecidos

Etapa 1. Use esta fórmula quando o problema informar a velocidade de um objeto e o tempo que leva
Alguns problemas matemáticos não dirão a que distância ou a que velocidade um objeto está se movendo. Você pode calcular o deslocamento usando essa magnitude de tempo e velocidade.
-
Nesse caso, a fórmula se torna: S = 1/2 (u + v) t.
U = velocidade inicial do objeto, ou a rapidez com que o objeto começa a se mover em uma determinada direção. V = velocidade final do objeto, ou quão rápido o objeto está se movendo em direção ao seu local final. T = o tempo que leva para o objeto atingir sua localização final.
- Exemplo: Um carro desce na estrada por 45 segundos (tempo necessário). O carro está virando para oeste a 20 m / s (velocidade inicial) e no final da estrada sua velocidade é de 23 m / s (velocidade final). Calcule o deslocamento com base nesses fatores.

Etapa 2. Insira a velocidade e o tempo necessários nas variáveis apropriadas
Agora que você sabe a distância que o carro está se movendo e a velocidade com que o carro está se movendo no início e no final, você pode encontrar a distância do local de partida ao local final.
Sua fórmula deve ser assim: S = 1/2 (20 + 23) 45

Etapa 3. Calcule a fórmula depois de colocar os valores no lugar correto
Lembre-se de seguir a ordem das operações, caso contrário, os deslocamentos resultarão em valores muito diferentes.
- Para esta fórmula, não importa se você acidentalmente trocar as velocidades inicial e final. Como você adicionará esses números primeiro, não importa onde eles estão entre parênteses. No entanto, para outras fórmulas, a troca das velocidades inicial e final resultará em diferentes valores de deslocamento.
- Sua fórmula deve ser semelhante a esta: S = 1/2 (43) 45. Primeiro divida 43 por 2, o que resulta em 21, 5. Em seguida, multiplique 21, 5 por 45, de modo que o resultado seja 967,5 metros. 967, 5 é a magnitude de seu deslocamento ou a distância que seu carro se moveu desde o ponto de partida.
Parte 3 de 5: quando a velocidade, aceleração e tempo iniciais são conhecidos
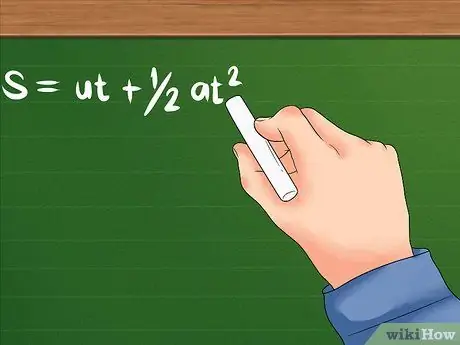
Etapa 1. Use a fórmula modificada quando a aceleração for conhecida além da velocidade e do tempo iniciais
Algumas perguntas dirão apenas a que velocidade o objeto está se movendo no início, a que velocidade o objeto está começando a acelerar e a que distância o objeto está se movendo. Você precisará da seguinte fórmula.
- A fórmula para esse problema é: S = ut + 1 / 2at². U ainda indica a velocidade inicial; a é a aceleração do objeto, ou quão rápido sua velocidade começa a mudar. T pode significar o tempo que leva ou uma certa quantidade de tempo que um objeto leva para acelerar. Ambos usarão unidades de tempo como segundos, horas e outros.
- Suponha que um carro se movendo a 25 m / s (velocidade inicial) comece a acelerar a 3 m / s2 (aceleração) por 4 segundos (tempo). Qual é o deslocamento do carro após 4 segundos?

Etapa 2. Insira os valores na fórmula
Ao contrário da fórmula anterior, apenas a velocidade inicial é representada aqui, portanto, certifique-se de inserir os dados corretos.
Com base nos dados de amostra acima, sua fórmula ficaria assim: S = 25 (4) + 1/2 (3) 4². Isso ajuda a adicionar parênteses em torno de sua magnitude de aceleração e tempo para ajudá-lo a separar os números
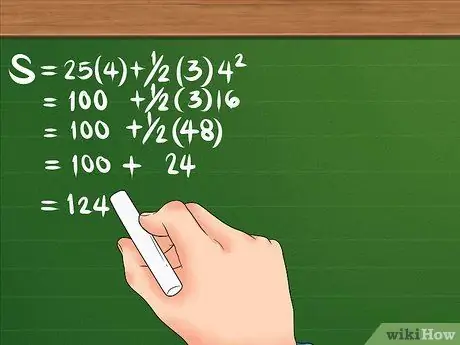
Etapa 3. Calcule o deslocamento fazendo-o na ordem correta de operações
Uma maneira rápida de ajudá-lo a lembrar a sequência de operações é a ponte burro Kur ir Kua ci Kadang Ba wa Juragan Turtles. Isso representa a ordem correta: parênteses, quadrados, multiplicação, divisão, adição e subtração.
Vejamos a fórmula novamente: S = 25 (4) + 1/2 (3) 4². Primeiro, quadrado 4, o resultado é 16. Em seguida, multiplique 16 por 3, resultando em 48; em seguida, multiplique também 25 por 4, para fazer 100. Divida 48 por 2, para fazer 24. Sua equação deve ficar assim: S = 100 + 24. Depois de somar os dois, o deslocamento é de 124 metros
Parte 4 de 5: Calculando o deslocamento angular

Etapa 1. Encontre o deslocamento angular conforme o objeto se move em um caminho circular
Embora você ainda esteja calculando o deslocamento usando uma linha reta, você precisará encontrar a diferença entre as localizações inicial e final do objeto à medida que ele se move em um caminho circular.
- Imagine uma garota sentada em um carrossel. Conforme ele gira com o carrossel, ele se moverá em um caminho circular. O deslocamento angular tenta encontrar a distância mais curta entre os locais inicial e final quando o objeto não está se movendo em linha reta.
- A fórmula para deslocamento angular é: = S / r, onde S é o deslocamento linear, r é o raio e é o deslocamento angular. O deslocamento linear é a distância que um objeto se move ao longo de um arco. O raio é a distância do objeto ao centro do círculo. O deslocamento angular é o valor que queremos encontrar.

Etapa 2. Insira o deslocamento linear e o raio na equação
Lembre-se de que o raio é a distância do centro do círculo; alguns problemas dirão o diâmetro de um círculo, que deve ser dividido por 2 para encontrar o raio.
- Aqui está um exemplo de problema: Uma garota anda em um carrossel. O assento está a 1 metro do centro do círculo (o raio). Se a menina está se movendo em uma trajetória de arco de 1,5 metros (deslocamento linear), qual é o seu deslocamento angular?
- Sua equação ficará assim: = 1,5 / 1.
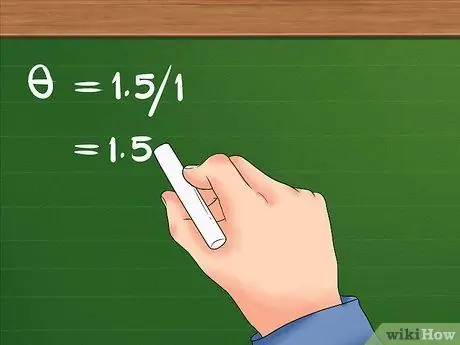
Etapa 3. Divida o deslocamento linear pelo raio
Esta divisão resultará no deslocamento angular do objeto.
- Depois de dividir 1,5 por 1, o resultado é 1,5. O deslocamento angular da menina é 1,5 radianos.
- Como o deslocamento angular mede o quanto um objeto gira desde sua posição inicial, ele deve ser medido como um ângulo, não como uma distância. Radiano é a unidade usada para medir ângulos.
Parte 5 de 5: Noções básicas sobre migração
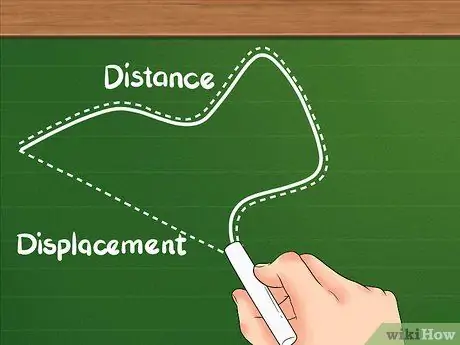
Etapa 1. Saiba que distância tem uma definição diferente de deslocamento
Distância mostra a distância total percorrida pelo objeto.
- A distância geralmente é conhecida como uma quantidade escalar. Distância mostra a distância percorrida por um objeto, independentemente da direção do objeto.
- Por exemplo, se você caminhar 2 passos para o leste, 2 passos para o sul, 2 passos para o oeste e, em seguida, 2 passos para o norte, você retornará à sua posição inicial. Mesmo que você tenha passado pelo total distância 10 passos de distância, você acabou de mover 0 passos de distância porque sua localização final é a mesma que sua localização inicial (seu caminho se assemelha a uma caixa).

Etapa 2. Entenda que o deslocamento é a diferença entre dois locais
O deslocamento não é a soma total do movimento como a distância; muda o foco na área entre os locais de partida e chegada.
- O deslocamento é chamado de quantidade vetorial e mostra a mudança na posição de um objeto considerando a direção do movimento do objeto.
- Por exemplo, você caminha para o leste por 5 passos. Se você voltar 5 passos para o oeste, você se moverá na direção oposta de seu local original. Mesmo que você tenha percorrido 10 etapas, sua posição não mudou; seu deslocamento é de 0 passos.

Etapa 3. Lembre-se das palavras para frente e para trás ao tentar imaginar o deslocamento
Mover-se na direção oposta elimina o deslocamento de um objeto.
Imagine um treinador de futebol para frente e para trás nos bastidores. Enquanto gritava com os jogadores, ele mudou da esquerda para a direita várias vezes. Se você observá-lo enquanto ele se move da esquerda para a direita, observará a distância total que ele percorreu. No entanto, suponha que o treinador pare para falar com o zagueiro nos bastidores. Se ele estiver em um ponto diferente de sua localização inicial antes de se mover, você estará observando o movimento do treinador

Etapa 4. Saiba que o deslocamento é medido usando um caminho reto, não um caminho circular
Para encontrar o deslocamento, você deve encontrar a maneira mais curta e eficiente de calcular a diferença entre dois pontos.
- Um caminho circular o levará do local inicial ao local final, mas não é o caminho mais curto. Para ajudá-lo a visualizá-lo, imagine que você está caminhando em linha reta e se depara com um pilar. Você não pode quebrar este pilar, então você o contorna. Mesmo que sua posição final seja a mesma como se você quebrasse o pilar, você precisará de etapas extras para atingir esse objetivo.
- Embora o deslocamento represente um caminho reto, saiba que você pode medir o deslocamento de um objeto que é Atualmente mover em um caminho circular. Esse deslocamento é chamado de deslocamento angular e pode ser calculado encontrando o caminho mais curto do local inicial ao local final.

Etapa 5. Saiba que o deslocamento pode ser negativo, ao contrário da distância
Se sua localização final for alcançada movendo-se na direção oposta à sua direção inicial, seu deslocamento será negativo.
- Por exemplo, caminhamos 5 passos para o leste e depois 3 passos para o oeste. Mesmo que por cálculo você se mova 2 passos de sua localização inicial, seu deslocamento é -2 porque você está se movendo na direção oposta. Sua distância sempre será positiva porque você não pode contar para trás em passos, quilômetros e assim por diante.
- O deslocamento negativo não significa que o deslocamento diminui. Negativo significa apenas que a direção é oposta.

Etapa 6. Perceba que às vezes a distância e o deslocamento podem ser iguais
Se você caminhar 25 passos em linha reta e parar, a distância percorrida será igual ao deslocamento de sua localização original.
- Isso se aplica apenas quando você se move de um local a partir do seu local de partida em linha reta. Por exemplo, você mora em San Francisco, Califórnia, e consegue um novo emprego em Las Vegas, Nevada. Você tem que se mudar para Las Vegas para estar perto de seu trabalho. Se você entrar em um avião que voa em linha reta de São Francisco a Las Vegas, você percorrerá a mesma distância e deslocamento x.
- No entanto, se você dirigir de São Francisco a Las Vegas, percorrerá uma distância x, mas percorrerá uma distância y. Como dirigir um carro geralmente tem direções variáveis (leste desta estrada, oeste dessa estrada), você viajará distâncias maiores do que a distância mais curta entre as duas cidades.






