- Autor Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-16 19:51.
- Última modificação 2025-01-23 12:43.
No estudo de instrumentos ópticos, a "ampliação" de um objeto semelhante a uma lente é a relação entre a altura da imagem que você vê e a altura real do objeto. Por exemplo, uma lente que pode fazer um objeto parecer muito grande tem um fator de ampliação "alto", enquanto uma lente que faz um objeto parecer pequeno tem um fator de ampliação "baixo". A fórmula para a ampliação de um objeto é geralmente calculada usando a fórmula M = (heu/ ho) = - (deu/ do), onde M = ampliação, heu = altura da imagem, ho = altura do objeto, e deu e Do = distância da imagem e do objeto.
Etapa
Método 1 de 2: cálculo da ampliação de lente única
Notas: A lente convergente mais largo no centro do que nas bordas (como uma lupa). uma lente divergente mais largo nas bordas do que no centro (como uma tigela). Calcular a ampliação em ambas as lentes é o mesmo, com uma exceção importante. Clique aqui para ir diretamente para as exceções para lentes divergentes.
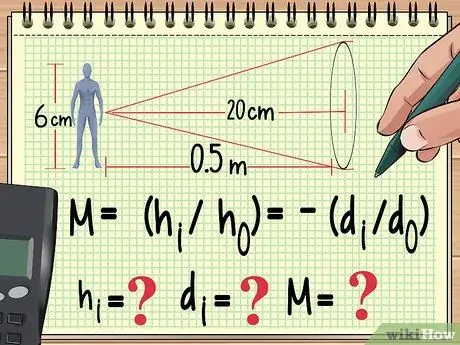
Etapa 1. Comece com sua equação e as variáveis que você já conhece
Assim como qualquer outro problema de física, a maneira de resolver um problema de ampliação é anotar a equação que você usará para calculá-lo. A partir daqui, você pode trabalhar para trás para encontrar o valor da variável que você não encontrou na equação que está usando.
-
Por exemplo, suponha que uma boneca de 6 cm de altura seja colocada a um metro de uma lente convergente com uma distância focal de 20 cm. Se quisermos calcular a ampliação, altura e distância da imagem, podemos começar a escrever nossa equação da seguinte forma:
-
- M = (heu/ ho) = - (deu/ do)
-
- Agora sabemos ho (altura da boneca) e do (distância da boneca da lente). Também sabemos a distância focal da lente, que não está nesta equação. Vamos contar heu, deu, e M.

Etapa 2. Usando a equação da lente para obter deu.
Se você conhece a distância do objeto que está ampliando e a distância focal da lente, calcular a distância da imagem formada é muito fácil com a equação da lente. A equação da lente é 1 / f = 1 / do + 1 / deu, onde f = comprimento focal da lente.
-
Neste exemplo de problema, podemos usar a equação da lente para calcular deu. Insira os valores de f e deu então resolva a equação:
-
- 1 / f = 1 / do + 1 / deu
- 1/20 = 1/50 + 1 / deu
- 5/100 - 2/100 = 1 / deu
- 3/100 = 1 / deu
- 100/3 = deu = 33,3 cm
-
- A distância focal da lente é a distância do centro da lente até o ponto onde a luz é transmitida no ponto focal. Se você já focalizou a luz com uma lente de aumento em formigas em chamas, você já viu. Nas perguntas da lição, geralmente a magnitude desse ponto de acesso foi fornecida. Na vida real, essas especificações são geralmente escritas em uma etiqueta localizada na lente.

Etapa 3. Calculando heu.
Depois de calcular do e Deu, você pode calcular a altura do objeto ampliado e a ampliação da lente. Observe os dois sinais de igual na equação de ampliação da lente (M = (heu/ ho) = - (deu/ do)) - isso significa que todas as partes desta equação são iguais, então podemos calcular M e heu na ordem que quisermos.
-
Para este problema de exemplo, podemos calcular heu assim:
-
- (heu/ ho) = - (deu/ do)
- (heu/6) = -(33, 3/50)
- heu = - (33, 3/50) x 6
- heu = - 3, 996 cm
-
- Observe que a altura do objeto aqui é negativa, o que indica que a imagem que veremos mais tarde será invertida (topo-base).

Etapa 4. Calculando M
Você pode calcular a última variável com a equação - (deu/ do) ou (heu/ ho).
-
No exemplo a seguir, como calcular M é o seguinte:
-
- M = (heu/ ho)
- M = (-3, 996/6) = - 0, 666
-
-
O resultado também será o mesmo quando calculado usando o valor de d:
-
- M = - (deu/ do)
- M = - (33, 3/50) = - 0, 666
-
- Observe que o zoom não tem um rótulo de unidade.
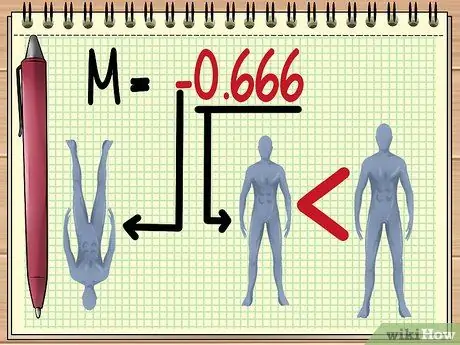
Etapa 5. Compreendendo o valor M
Depois de obter a magnitude do valor M, você pode estimar várias coisas sobre a imagem que verá através das lentes, a saber:
-
O tamanho.
Quanto maior o "valor absoluto" de M, maior será o objeto visto com a lente. O valor M entre 0 e 1 indica que o objeto parecerá menor.
-
Orientação do objeto.
Um valor negativo indica que a imagem formada será invertida.
- No exemplo dado aqui, o valor M de -0,666 significa que, de acordo com o valor da variável existente, a sombra do boneco ficará visível. de cabeça para baixo e dois terços menor que o tamanho real.
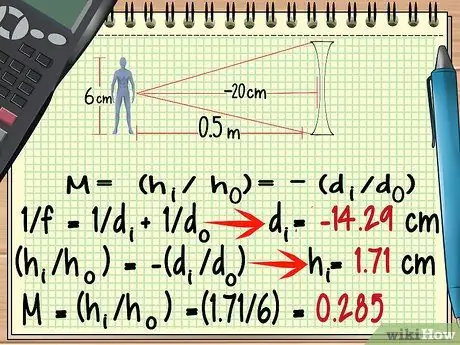
Etapa 6. Para lentes divergentes, use um ponto focal negativo
Embora o formato de uma lente divergente seja muito diferente do formato de uma lente convergente, você pode calcular sua ampliação usando a mesma fórmula acima. As exceções a serem lembradas são O ponto focal da lente divergente é negativo.
No exemplo do problema acima, isso afetará a resposta que você obterá ao calcular deu, portanto, preste atenção a isso.
-
Vamos retrabalhar o problema do exemplo acima, só que agora usamos uma lente divergente com comprimento focal - 20 cm.
As outras variáveis permanecem com o mesmo valor.
-
Em primeiro lugar, vamos calcular deu usando a equação da lente:
-
- 1 / f = 1 / do + 1 / deu
- 1 / -20 = 1/50 + 1 / deu
- -5/100 - 2/100 = 1 / deu
- -7/100 = 1 / deu
- -100/7 = deu = - 14, 29 cm
-
-
Agora vamos calcular heu e M com um valor de deu o novo.
-
- (heu/ ho) = - (deu/ do)
- (heu/6) = -(-14, 29/50)
- heu = - (- 14, 29/50) x 6
- heu = 1, 71 cm
- M = (heu/ ho)
- M = (1, 71/6) = 0, 285
-
Método 2 de 2: Calculando a Ampliação de Múltiplas Lentes
Método Simples de Duas Lentes
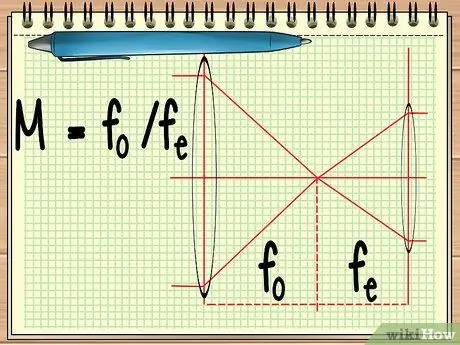
Etapa 1. Calcule o ponto focal das duas lentes
Quando você usa um instrumento que consiste em duas lentes dispostas lado a lado (como um telescópio ou um par de binóculos), tudo o que você precisa descobrir é o ponto focal das duas lentes para calcular a ampliação geral das duas lentes. isso pode ser calculado pela equação simples M = fo/ fe.
Na equação, fo é o ponto focal da lente objetiva e fe é o ponto focal da ocular. A lente objetiva é a lente grande que está perto do objeto, enquanto a lente ocular é a lente que está localizada perto do olho do observador.

Etapa 2. Insira as informações que você já possui na equação M = fo/ fe.
Depois de ter os pontos focais de ambas as lentes, é muito fácil calculá-los, - calcule a proporção dividindo a distância focal da lente objetiva pela distância focal da ocular. A resposta que você obtém é a ampliação total da ferramenta.
-
Por exemplo, suponha um telescópio simples, está escrito que o ponto focal da lente objetiva é 10cm e o ponto focal da ocular é 5cm, então a ampliação é 10/5 = 2.
Método Complicado
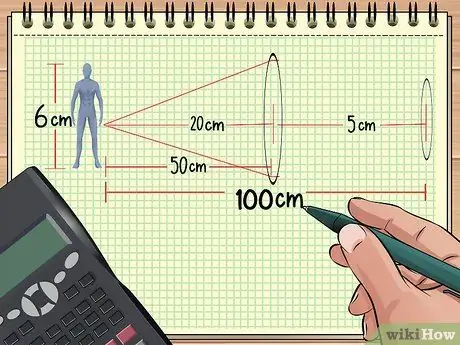
Etapa 1. Calcule a distância entre as lentes e o objeto
Se você tiver duas lentes dispostas em uma linha na frente de um objeto, a ampliação total pode ser calculada se você souber a distância das lentes ao objeto, o tamanho do objeto e o ponto focal das duas lentes. O restante também pode ser calculado.
Por exemplo, suponha que organizamos objetos e lentes como no exemplo do problema 1 acima: uma boneca está a 50 cm de uma lente convergente que tem uma distância focal de 20 cm. Agora, posicione a segunda lente com ponto focal 5 cm a uma distância de 50 cm da primeira lente (100 cm do boneco). Em seguida, calcularemos a ampliação total a partir das informações que obtivemos
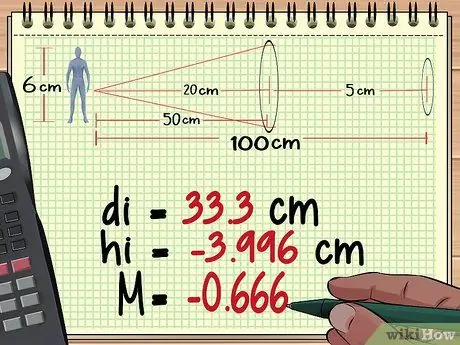
Etapa 2. Calcule a distância, altura e ampliação do objeto com a lente 1
A primeira parte do cálculo da ampliação de lentes múltiplas é o mesmo que calcular a ampliação de uma única lente. Comece com a lente mais próxima do objeto, use a equação da lente para encontrar a distância da imagem formada e, em seguida, use a equação de ampliação para encontrar a altura e a ampliação da imagem. Clique aqui para ver mais cálculos de ampliação de lente única.
-
A partir de nossos cálculos no Método 1 acima, descobrimos que a primeira lente produz uma imagem tão alta quanto - 3, 996 cmdistância 33,3 cm atrás da lente, e com uma ampliação de - 0, 666.
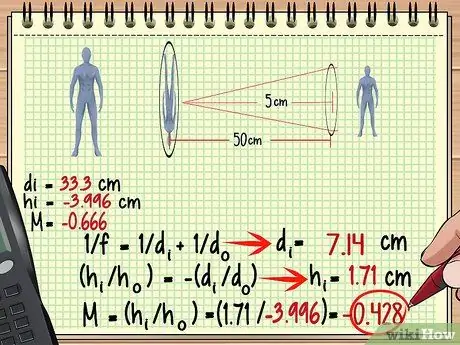
Etapa 3. Use a imagem da primeira lente como o objeto da segunda lente
Agora, encontrar a ampliação, altura e muito mais para a segunda lente é muito fácil - basta usar o mesmo método que você usou para a primeira lente, mas desta vez trate a imagem como um objeto. Lembre-se de que a distância da imagem até a segunda lente nem sempre é a mesma que a distância do objeto até a primeira lente.
-
No exemplo acima, uma vez que a imagem é formada 33,3 cm atrás da primeira lente, a distância é de 50-33,3 = 16,7 cm na frente da segunda lente. Vamos usar essa medida e o comprimento focal da segunda lente para encontrar a imagem formada pela segunda lente.
-
- 1 / f = 1 / do + 1 / deu
- 1/5 = 1/16, 7 + 1 / deu
- 0, 2 - 0, 0599 = 1 / deu
- 0, 14 = 1 / deu
- deu = 7, 14 cm
-
-
Agora podemos calcular heu e M para a segunda lente:
-
- (heu/ ho) = - (deu/ do)
- (heu/-3, 996) = -(7, 14/16, 7)
- heu = - (0, 427) x -3, 996
- heu = 1, 71 cm
- M = (heu/ ho)
- M = (1, 71 / -3, 996) = - 0, 428
-
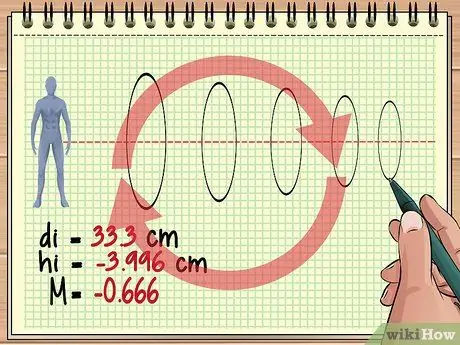
Etapa 4. Continue calculando assim para as lentes adicionais
Essa abordagem básica é a mesma se houver três, quatro ou centenas de lentes alinhadas na frente de um objeto. Para cada lente, considere a imagem da lente anterior como o objeto e use a equação da lente e a equação de ampliação para encontrar a resposta desejada.
Lembre-se de que cada lente subsequente pode inverter continuamente a imagem formada. Por exemplo, o valor de ampliação que obtivemos anteriormente (-0, 428) indica que a imagem que veremos é de aproximadamente 4/10 do tamanho real do objeto, mas perpendicular, porque a imagem da lente anterior está invertida
Pontas
- Os binóculos geralmente fornecem uma explicação das especificações de ampliação na forma de um número vezes outro número. Por exemplo, os binóculos podem ser especificados como 8x25 ou 8x40. Quando escrito assim, o primeiro número é a ampliação dos binóculos. Não importa mesmo se no exemplo dado, os dois números são diferentes em magnitude, ambos os binóculos têm uma ampliação de 8 vezes. O segundo número indica o quão clara a imagem será formada pelos binóculos.
- Lembre-se de que para a lupa de lente única, a ampliação será negativa se a distância do objeto for maior do que a distância focal da lente. Isso não significa que a imagem formada será menor. Nesse caso, a ampliação ainda ocorre, mas a imagem formada será vista de cabeça para baixo (de cima para baixo) pelo observador.






