- Autor Jason Gerald [email protected].
- Public 2024-01-15 08:22.
- Última modificação 2025-01-23 12:43.
O valor P é uma medida estatística que ajuda os cientistas a determinar se suas hipóteses estão corretas. O valor P é usado para determinar se os resultados de seu experimento estão dentro da faixa de valores que são normais para as coisas estudadas. Normalmente, se o valor P de um conjunto de dados cair abaixo de um certo valor predeterminado (por exemplo, 0,05), os cientistas rejeitarão a hipótese nula de seu experimento - em outras palavras, eles irão descartar uma hipótese onde a variável experimental foi nenhum efeito significativo no resultado. Hoje, os valores de p são geralmente encontrados em tabelas de referência, calculando o valor do qui quadrado.
Etapa

Etapa 1. Determine os resultados esperados de seu experimento
Normalmente, quando os cientistas conduzem um experimento e examinam os resultados, eles já têm uma ideia dos resultados normais ou ordinários de antemão. Isso pode ser baseado nos resultados de experimentos anteriores, conjuntos de dados observacionais confiáveis, literatura científica e / ou outras fontes. Para sua experiência, determine o resultado esperado e anote-o como um número.
Exemplo: suponha que um estudo anterior mostrasse que, em nível nacional, as multas por excesso de velocidade eram emitidas com mais frequência para carros vermelhos do que para carros azuis. Suponha que o resultado médio em nível nacional mostre uma proporção de 2: 1 com a proporção de carros vermelhos sendo maior. Queremos saber se os policiais de nossa cidade também obtêm a mesma tendência, analisando a multa de velocidade emitida pela polícia de nossa cidade. Se tivéssemos uma amostra aleatória de 150 multas por excesso de velocidade dadas a carros vermelhos e azuis em nossa cidade, seria de esperar 100 para carro vermelho e 50 para carros azuis se a unidade policial de nossa cidade dá uma multa de acordo com a comparação em nível nacional.

Etapa 2. Determine suas observações experimentais
Agora que você determinou seu valor esperado, pode executar seu experimento e encontrar o valor verdadeiro (ou observação). Novamente, anote o resultado como um número. Se manipularmos algumas condições experimentais e os resultados observados diferirem dos resultados esperados, existem duas possibilidades: ou isso aconteceu por acaso, ou foi a nossa manipulação das variáveis experimentais que causou essa diferença. O propósito de encontrar o valor p é basicamente determinar se os resultados observados diferem dos resultados esperados a um ponto em que a hipótese nula - a hipótese de que não há relação entre a variável experimental e os resultados observados - não pode ser rejeitada.
Exemplo: Suponha que, em nossa cidade, selecionemos aleatoriamente 150 multas por excesso de velocidade que são concedidas a carros vermelhos e azuis. Nós temos 90 uma passagem para um carro vermelho e 60 para o carro azul. Isso é diferente do resultado que esperávamos, ou seja, 100 e 50. Nossa manipulação experimental (neste caso, mudar a fonte de dados de nacional para local) causou alguma mudança nos resultados, ou nossa polícia municipal tinha as mesmas tendências do nível nacional, e apenas observamos coincidência? O valor de p nos ajudará a determiná-lo.

Etapa 3. Determine os graus de liberdade de seu experimento
Os graus de liberdade são uma medida da quantidade de variabilidade no estudo, que é determinada pelo número de categorias que você examina. A equação para os graus de liberdade é Graus de liberdade = n-1, onde n é o número de categorias ou variáveis analisadas em seu experimento.
-
Exemplo: Nosso experimento tem duas categorias de resultados: uma para o carro vermelho e outra para o carro azul. Assim, em nosso experimento, temos 2-1 = 1 grau de liberdade.
Se compararmos carros vermelhos, azuis e verdes, teremos
Passo 2. graus de liberdade e assim por diante.

Etapa 4. Compare os resultados esperados com os resultados observados usando qui quadrado
Chi ao quadrado (escrito x2) é um valor numérico que mede a diferença entre os valores esperados e observados do experimento. A equação para chi ao quadrado é: x2 = ((o-e)2/ e), onde o é o valor observado e e é o valor esperado. Some os resultados desta equação para todos os resultados possíveis (veja abaixo).
- Observe que esta equação usa o operador (sigma). Em outras palavras, você deve calcular ((| o-e | -.05)2/ e) para cada resultado possível e, em seguida, some os resultados para obter o valor do qui quadrado. Em nosso exemplo, temos dois resultados - um carro que recebe uma multa vermelha ou azul. Assim, podemos calcular ((o-e)2/ e) duas vezes - uma para o carro vermelho e uma vez para o carro azul.
-
Exemplo: vamos inserir nossos valores esperados e observações na equação x2 = ((o-e)2/ e). Lembre-se de que, por causa do operador sigma, temos que calcular ((o-e)2/ e) duas vezes - uma para o carro vermelho e uma vez para o carro azul. As etapas de processamento são as seguintes:
- x2 = ((90-100)2/100) + (60-50)2/50)
- x2 = ((-10)2/100) + (10)2/50)
- x2 = (100/100) + (100/50) = 1 + 2 = 3.

Etapa 5. Escolha um nível de significância
Agora que sabemos os graus de liberdade de nosso kit experimental e o valor do qui quadrado, há apenas uma última coisa que precisamos fazer antes de encontrar nosso valor p - precisamos determinar o nível de significância. Basicamente, o nível de significância é uma medida de quão seguros estamos de nossos resultados - um baixo nível de significância corresponde a uma baixa probabilidade de que o resultado de um experimento foi devido ao acaso e vice-versa. O nível de significância é escrito como um decimal (por exemplo, 0,01), que corresponde à chance percentual de que o resultado do experimento foi devido ao acaso (neste caso, 1%).
- Por convenção, os cientistas geralmente definem um valor de significância para seus experimentos em 0,05 ou 5 por cento. Isso significa que os resultados experimentais que correspondem a esse nível de significância têm, no máximo, 5% de chance de coincidência. Em outras palavras, há 95% de chance de que os resultados sejam decorrentes da manipulação do cientista das variáveis experimentais, e não do acaso. Para a maioria dos experimentos, 95% de confiança sobre a relação entre as duas variáveis é considerada bem-sucedida na demonstração da relação entre as duas.
- Exemplo: para nosso exemplo de carro vermelho e azul, vamos seguir o acordo científico e determinar nosso nível de significância de 0, 05.
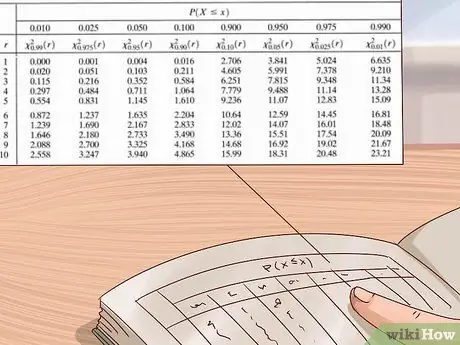
Etapa 6. Use a tabela de distribuição do qui-quadrado para estimar seu valor p
Cientistas e estatísticos usam grandes tabelas de valores para calcular os valores de p para seus experimentos. Esta tabela é geralmente escrita com o eixo vertical à esquerda mostrando os graus de liberdade e o eixo horizontal no topo mostrando os valores p. Use esta tabela encontrando primeiro os seus graus de liberdade e, em seguida, lendo as linhas da esquerda para a direita até encontrar o primeiro valor que é maior do que o seu valor qui quadrado. Observe o valor p no topo da coluna - seu valor p está entre este valor e o próximo maior valor (o valor direito está à esquerda dele).
- As tabelas de distribuição de qui-quadrado estão disponíveis em uma variedade de fontes - elas podem ser facilmente encontradas online ou em livros de ciências ou estatística. Se você não tiver uma, use a tabela mostrada na foto acima ou uma tabela online gratuita, como a fornecida por medcalc.org aqui.
-
Exemplo: Nosso qui quadrado é 3. Portanto, vamos usar a tabela de distribuição do qui quadrado na foto acima para encontrar um valor p aproximado. Uma vez que sabemos que nosso experimento só
Passo 1. graus de liberdade, começaremos da mesa superior. Vamos da esquerda para a direita nesta linha até encontrar um valor maior que
Etapa 3. - nosso valor chi quadrado. O primeiro valor que encontramos é 3,84. Olhando para cima nesta coluna, vemos que o valor p correspondente é 0,05. Isso significa que nosso valor p é entre 0,05 e 0,1 (próximo maior valor p na tabela).

Etapa 7. Decida se rejeita ou defende sua hipótese nula
Como você encontrou um valor p aproximado para seu experimento, pode decidir se rejeita ou não a hipótese nula de seu experimento (como um lembrete, esta é a hipótese de que a variável experimental que você manipulou não teve efeito nos resultados observados). Se o seu valor p for inferior ao seu valor de significância, parabéns - você provou que há uma grande probabilidade de que haja uma relação entre as variáveis que você manipulou e suas observações. Se o seu valor p for maior do que o seu valor de significância, você não pode dizer com certeza que os resultados que está observando são o resultado de mera coincidência ou manipulação de seu experimento.
- Exemplo: nosso valor p está entre 0,05 e 0,1. Ou seja, não é de forma alguma inferior a 0,05, então, infelizmente, nós não pode rejeitar nossa hipótese nula. Isto significa que não atingimos o limite mínimo de confiança de 95% que estabelecemos para que se possa dizer que a polícia da nossa cidade concede multas a carros vermelhos e azuis numa proporção bastante diferente da média nacional.
- Em outras palavras, existe uma chance de 5 a 10% de que nossas observações não sejam o resultado de uma mudança na localização (analisando nossa cidade, e não a parte inteira), mas sejam coincidências. Uma vez que estamos procurando uma probabilidade de menos de 5%, não podemos dizer que convencido que a polícia em nossa cidade tende a multar carros vermelhos - há uma possibilidade pequena, mas estatisticamente muito diferente, de que eles não tenham essa tendência.
Pontas
- Uma calculadora científica tornará os cálculos muito mais fáceis. Você também pode pesquisar calculadoras online.
- Você pode calcular os valores p usando vários programas de computador, incluindo software de planilha comumente usado e software estatístico mais especializado.






