- Autor Jason Gerald [email protected].
- Public 2024-01-19 22:13.
- Última modificação 2025-01-23 12:43.
Beta é a volatilidade, ou risco, de uma determinada ação em relação à volatilidade de todo o mercado de ações. O beta é um indicador de quão arriscado uma determinada ação é e é usado para avaliar sua taxa de retorno esperada. Beta é um dos princípios básicos que os analistas de ações consideram ao selecionar ações para seus portfólios, junto com a relação preço / lucro, patrimônio líquido, índice dívida / patrimônio e outros fatores.
Etapa
Parte 1 de 4: Calculando Beta Usando Equações Simples

Etapa 1. Encontre o nível da proporção livre de risco
Esta é a taxa de retorno que os investidores esperam dos investimentos cujo dinheiro não é arriscado. Este valor é geralmente expresso como uma porcentagem.

Etapa 2. Determine o nível de cada índice representativo
Esses números também são expressos em porcentagem. Normalmente, a taxa de retorno é de vários meses.
Um ou ambos os valores podem ser negativos, significando que o investimento em ações ou mercado (índice) como um todo sofreu uma perda em relação ao investimento no período. Se apenas 1 dos 2 níveis for negativo, o beta será negativo

Etapa 3. Subtraia a taxa livre de risco da taxa de retorno da ação
Se a taxa de retorno da ação for 7% e a taxa livre de risco for 2%, a diferença será de 5%.

Etapa 4. Subtraia a relação livre de risco da taxa de retorno do mercado (ou índice)
Se o preço de mercado ou índice de retorno for de 8% e a taxa livre de risco for novamente de 2%, a diferença será de 6%.

Etapa 5. Divida a diferença na taxa de retorno da ação menos a taxa livre de risco pelo mercado (ou índice), a taxa de retorno menos a taxa livre de risco
Esta é uma versão beta, que geralmente é expressa como um valor decimal. No exemplo acima, beta seria 5 dividido por 6, ou 0,833.
- O beta do próprio mercado, ou o índice que ele representa, é 1,0, porque o mercado está sendo comparado a si mesmo e o número zero dividido por si é igual a 1. Um beta menor que 1 significa que a ação é menos volátil do que o mercado, pois um todo, enquanto um beta maior que 1 significa que a ação é mais estável do que o mercado como um todo. O valor beta pode ser menor que zero, o que significa que a ação está perdendo dinheiro enquanto o mercado como um todo está ganhando dinheiro ou a ação está ganhando dinheiro temporário e o mercado como um todo está perdendo dinheiro.
- Ao procurar o beta, embora não seja obrigatório, é comum usar um índice representativo do mercado em que a ação está sendo negociada. Para ações negociadas internacionalmente, o MSCI EAFE (que representa a Europa, a Australásia e o Oriente) é um índice representativo adequado.
Parte 2 de 4: Usando Beta para Determinar a Taxa de Câmbio de Retorno

Etapa 1. Encontre o nível da proporção livre de risco
Este é o mesmo valor descrito acima em "Cálculo do beta para uma ação". Para esta seção, usaremos o mesmo valor do exemplo de 2 por cento, conforme usado acima.

Etapa 2. Determine a taxa de retorno do mercado ou um índice representativo
Neste exemplo, usaremos o mesmo número 8 por cento, conforme usado acima.

Etapa 3. Multiplique o valor beta pela diferença entre a taxa de retorno do mercado e a taxa livre de risco
Por exemplo, usaremos um valor beta de 1,5. Usando 2% para a taxa livre de risco e 8% para a taxa de retorno do mercado, isso resulta em 8-2, ou 6%. Multiplicado por um beta de 1,5, rende 9 por cento.
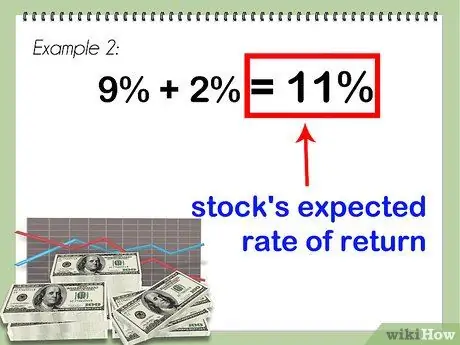
Etapa 4. Adicione o resultado com a taxa livre de risco
Ela rende 11%, que é a taxa de retorno esperada da ação.
Quanto maior o valor beta da ação, maior a taxa de retorno esperada. No entanto, essa taxa de retorno mais alta está associada a um risco maior, por isso é necessário olhar para outras ações fundamentais antes de considerar se elas devem fazer parte da carteira de um investidor
Parte 3 de 4: Usando gráficos do Excel para determinar o beta
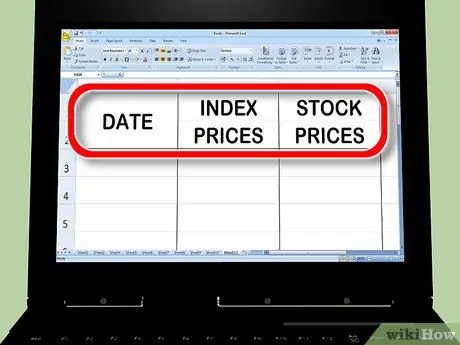
Etapa 1. Crie três colunas de preços no Excel
A primeira coluna é a data. Na segunda coluna, coloque o preço do índice; este é o "mercado geral" com o qual você comparará os betas. Na terceira coluna, coloque o preço representativo da ação para o qual você está tentando calcular o beta.
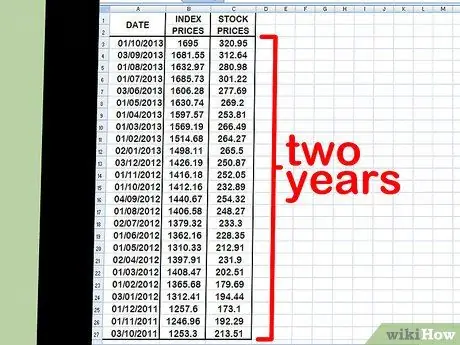
Etapa 2. Coloque seus pontos de dados em uma planilha
Tente começar em intervalos de um mês. Escolha uma data - por exemplo, no início ou no final do mês - e insira o valor apropriado para o índice do mercado de ações (tente usar o S&P 500) e, em seguida, o estoque representativo para esse dia. Tente escolher as últimas 15 ou 30 datas, talvez estendendo-se por um ou dois anos no passado. Preste atenção ao preço do índice e ao preço das ações representativas para essa data.
Quanto mais tempo você escolher, mais preciso será o cálculo do beta. O beta muda conforme você monitora ações e índices por um longo tempo
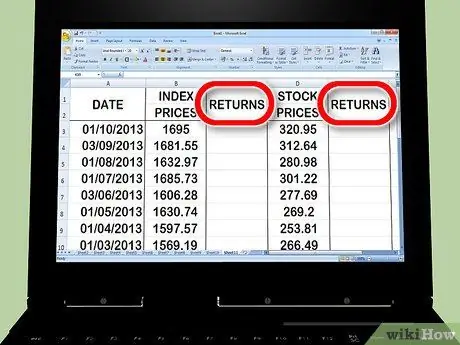
Etapa 3. Crie duas colunas de volta à direita da coluna de preço
Uma coluna retornará o índice; a segunda coluna é o estoque. Você usará fórmulas do Excel para redefinir o que aprenderá nas etapas a seguir.
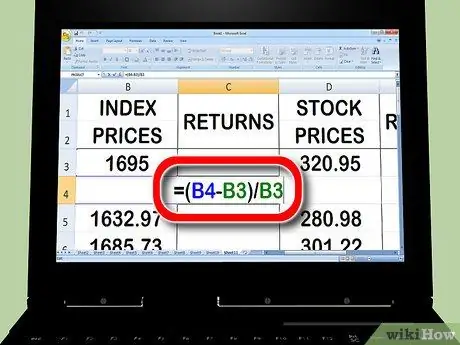
Etapa 4. Comece a calcular de volta para o índice do mercado de ações
Na segunda célula da coluna de índice digite =. Com o cursor, clique na segunda célula da coluna do índice, digite - e clique na primeira célula da coluna do índice. Em seguida, digite / e clique na primeira célula da coluna de índice novamente. pressione Return ou Enter.
- Ao recalcular ao longo do tempo, você não insere nada na primeira célula; deixe em branco. Você precisa de pelo menos dois pontos de dados para recalcular, por isso você começará na segunda célula da coluna do índice.
- O que você faz é subtrair o novo valor do valor antigo e, em seguida, dividir o resultado pelo valor antigo. Isso é para que você saiba qual foi a porcentagem de perda ou ganho no período.
- Sua equação na coluna de retorno pode ser assim: = (B3-B2) / B2
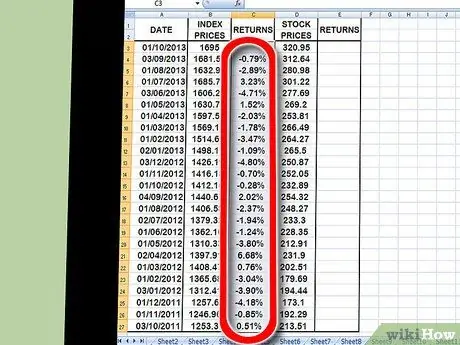
Etapa 5. Use a função de cópia para repetir este processo para todos os pontos de dados na coluna de índice de preços
Faça isso clicando no pequeno quadrado na parte inferior direita da célula do índice e, em seguida, arraste-o para o ponto de dados mais inferior. O que você faz é pedir ao Excel para replicar a mesma fórmula usada para cada ponto de dados diferente.
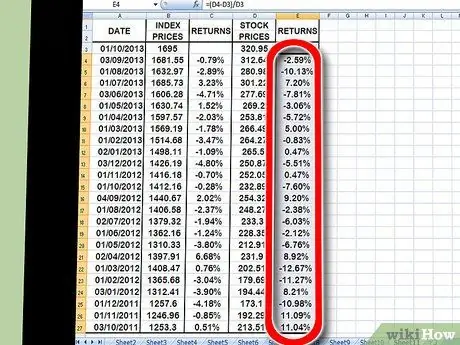
Etapa 6. Repita exatamente o mesmo processo para os retornos, desta vez para ações individuais, não índices
Quando terminar, você terá duas colunas, formatadas como porcentagem, que listam os retornos para cada índice de ações e ações individuais.
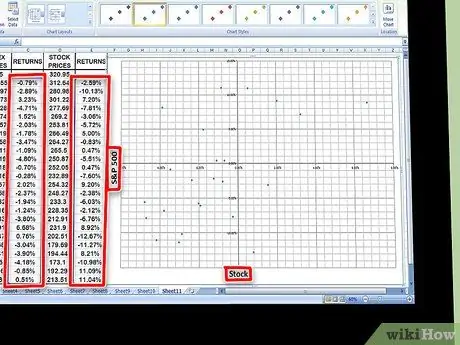
Etapa 7. Plote os dados em uma tabela
Destaque todos os dados nas duas colunas de retorno e clique no ícone Gráfico no Excel. Selecione o gráfico de dispersão na lista de opções. Nomeie o eixo X como o índice que você está usando (por exemplo, S&P 500) e o eixo Y como o estoque que você está usando.
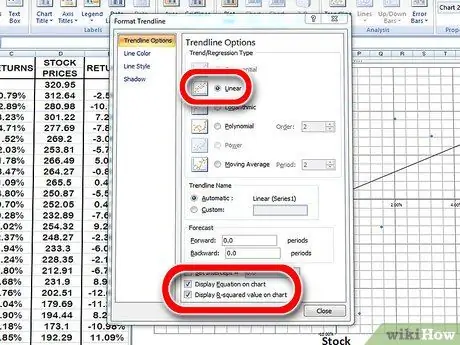
Etapa 8. Adicione uma linha de tendência ao seu gráfico de dispersão
Você também pode fazer isso selecionando um layout de linha de tendência em versões mais recentes do Excel ou especificando-o manualmente clicando em Gráfico → adicionar linha de tendência. Certifique-se de exibir a equação na tabela. 2 valores.
- Certifique-se de escolher uma linha de tendência linear, não um polinômio ou uma média.
- A exibição da equação em uma tabela depende da versão do Excel que você possui. As versões mais recentes do Excel permitirão o gráfico de equação clicando em Layout rápido do gráfico.
- Nesta versão do Excel, aponte para Gráfico; Adicionar Trendline; opções. Em seguida, marque as duas caixas ao lado de "Exibir equação no gráfico".
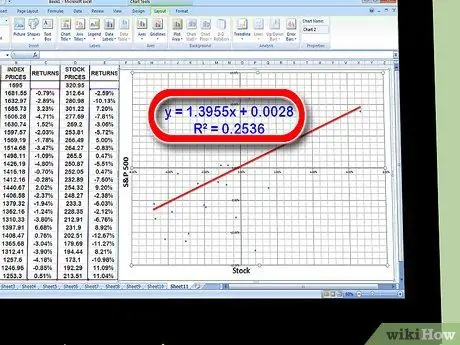
Etapa 9. Encontre o coeficiente para o valor "x" na equação da linha de tendência
Sua equação de linha de tendência será escrita na forma "y = x + a". O coeficiente do valor x é beta.
Parte 4 de 4: Compreendendo o Beta

Etapa 1. Como interpretar o beta
Beta é o risco para o mercado de ações como um todo, com o investidor assumindo a propriedade de uma determinada ação. É por isso que você precisa comparar a taxa de retorno de uma única ação com o retorno do índice - o índice de referência. O risco do índice permanece em 1. Um beta “baixo” de 1 significa que a ação é menos arriscada do que o índice que está sendo comparado. Um beta “alto” de 1 significa que a ação é mais arriscada do que o índice com o qual está sendo comparada.
- Veja este exemplo. Digamos que o beta do Gino Germ seja calculado em 0,5. Comparado com o S&P 500, o benchmark que Gino está comparando é "metade" tão arriscado. Se o S&P ficar abaixo de 10%, o preço das ações de Gino tenderá a cair apenas 5%.
- Como outro exemplo, imagine que o serviço Funeral de Frank tem um beta de 1,5 em comparação com o S&P. Se o S&P cair 10%, espere que o preço das ações de Frank caia "mais" do que o S&P, ou cerca de 15%.

Etapa 2. O risco também está associado aos retornos
Alto risco, alta recompensa; baixo risco, baixa recompensa. Uma ação com um beta baixo não perderá tanto quanto o S&P quando cair, mas também não ganhará tanto quanto o S&P quando apresentar ganhos. Por outro lado, uma ação com um beta acima de 1 perderá mais do que o S&P quando cair, mas também ganhará mais do que o S&P quando for lançada.
Por exemplo, a Vermeer Venom Extraction tem um beta de 0,5. Quando o mercado de ações sobe 30%, a Vermeer obtém apenas 15% de lucro. Mas quando o mercado de estoque do depósito é de 30%, a Vermeer obtém apenas 15% do estoque do depósito

Etapa 3. Saiba que as ações com beta 1 se moverão em linha com o mercado
Se você fizer um cálculo de beta e conhecer a ação, você analisa quando ela tem beta 1, não haverá mais nem menos risco do que o índice usado como benchmark. O mercado subiu 2%, seu estoque subiu 2%; o mercado caiu 8%, seu estoque caiu 8%.
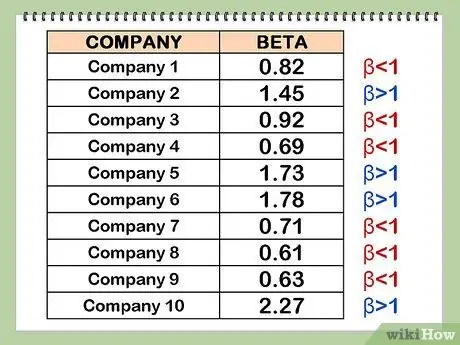
Etapa 4. Inclua ações de beta alto e baixo em seu portfólio para diversificação
Se for uma boa combinação de altos e baixos, o beta o ajudará a analisar se o valor do mercado de ações está caindo drasticamente. Obviamente, como as ações com beta baixo geralmente apresentam desempenho inferior ao do mercado de ações em um determinado período, uma boa combinação de betas também significa que você não terá o preço das ações particularmente alto.

Etapa 5. Reconheça que, como a maioria das ferramentas de previsão financeira, os betas podem não prever totalmente o futuro
O beta realmente mede a volatilidade passada de uma ação. Geralmente, os projetos apresentam volatilidade no futuro, mas nem sempre são precisos. O beta pode mudar drasticamente de um ano para o outro. Usar o beta histórico de uma ação pode nem sempre ser uma maneira precisa de prever a volatilidade atual.
Sugestão
- Observe que a teoria de covariância clássica pode não se aplicar por causa da série de tempo financeiro Cauda pesada”. Na verdade, o desvio padrão e a média para a distribuição subjacente podem não existir! Portanto, talvez uma modificação usando spreads de quartil e mediana em vez de média e desvio padrão possa funcionar.
- O beta analisa a volatilidade de uma ação ao longo de um determinado período de tempo, independentemente de o mercado estar em alta ou em baixa. Como outros fundamentos de ações, analisar o desempenho passado não é garantia de como as ações irão se comportar no futuro.






