- Autor Jason Gerald [email protected].
- Public 2024-01-19 22:13.
- Última modificação 2025-01-23 12:43.
Valor de posição, ou o conceito de que o valor de um número (0-9) é determinado por sua posição em um número particular, é um conceito fundamental em matemática. Como esse conceito é tão fácil para pessoas que já o entendem, ensiná-lo pode ser bem complicado. No entanto, uma vez que os alunos entendam esse conceito, eles estarão prontos e animados para usar suas novas habilidades e aprender conceitos matemáticos mais complexos.
Etapa
Parte 1 de 3: Apresentando os conceitos básicos

Etapa 1. Reserve um tempo para ensinar o valor posicional
Se você leciona dentro de um escopo de currículo predefinido, você já deve ter uma ideia de como encaixar valor de posição em uma gama mais ampla de aprendizagem. Se você for tutor ou lecionar em casa, a estrutura de aprendizagem será mais flexível. Planeje ensinar valor posicional algum tempo depois que os alunos terminarem de aprender a contar e realizar operações simples de adição e subtração - geralmente por volta da 1ª ou 2ª série. A compreensão do valor posicional fornecerá uma base para que essas crianças entendam conceitos matemáticos mais complexos.

Etapa 2. Apresente o conceito de contagem de grupos de números
A maioria dos alunos das crianças só aprende a contar os números um por um: um … dois … três … quatro. Isso é suficiente para adição e subtração básicas, mas ainda é muito simples para fornecer uma base sólida para a compreensão de funções mais complexas. Antes de ensiná-los a decompor grandes números em seus respectivos valores nominais, é uma boa ideia ensiná-los a dividir um grupo de pequenos números em grandes números.
- Ensine seus alunos a contar dois, dois, três, três, cinco, cinco e dez dez. Este é um conceito fundamental para os alunos entenderem antes de aprenderem sobre o valor posicional.
- Em particular, tente construir uma forte "emoção de dezenas". A matemática moderna usa o número dez como base, tornando mais fácil para as crianças aprenderem sistemas mais complexos se elas se acostumarem a pensar dessa maneira. Ensine seus alunos a agrupar instintivamente os números em conjuntos de dez.

Etapa 3. Revise o conceito de valor posicional
Renove sua compreensão. Certifique-se de compreender totalmente este conceito antes de tentar ensiná-lo a um grupo de jovens alunos. Simplificando, o valor posicional é a ideia de que o valor de um número (0-9) depende de seu "lugar" ou posição em um número.

Etapa 4. Explique a diferença entre números e números
Números são símbolos dos dez números básicos que compõem todos os números: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Esses números são combinados para formar todos os outros números. Um número pode ser um número (por exemplo, o número 7), mas apenas se não estiver agrupado com outros números. Quando dois ou mais números são agrupados, a sequência dos números forma o número maior.
Mostre que por si só "1" é o número um e "7" é o número sete. Quando agrupados como "17", os dois números formam o número dezessete. Da mesma forma, "3" e "5" juntos formam o número trinta e cinco. Mostre alguns outros exemplos para que os alunos possam ir para casa entendendo
Parte 2 de 3: Ensino por Exemplos Visuais
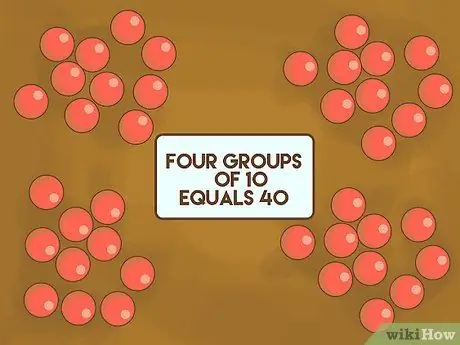
Passo 1. Mostre às crianças que contar de dez a dez é mais fácil
Use de 30 a 40 objetos pequenos, contáveis e razoavelmente homogêneos. Por exemplo: seixos, mármores ou uma borracha. Espalhe na mesa em frente aos alunos. Explique que na matemática moderna, usamos o número 10 como base. Organize os objetos em vários grupos e conte-os na frente da classe. Mostre a eles que quatro grupos de 10 pedras equivalem a 40.

Etapa 2. Traduzir o exemplo com pedras em números escritos
Escreva o esboço do conceito na lousa. Primeiro, crie um gráfico T regular. Escreva o número 1 no canto superior direito da tabela T. Em seguida, escreva o número 10 no canto superior esquerdo. Escreva um 0 na coluna à direita denominada "1" e escreva 4 na coluna à esquerda denominada "10". Agora você pode explicar para a classe que cada número feito com pedras tem seu próprio "lugar".
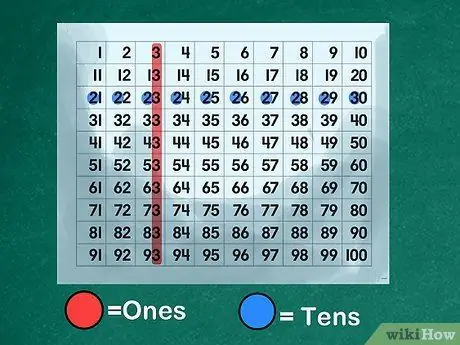
Etapa 3. Use um teclado numérico para ilustrar a base do valor posicional
Crie ou imprima um "teclado numérico" que exiba todos os números em ordem de 1 a 100. Mostre aos alunos como os números de 0 a 9 interagem com os números de 10 a 100. Explique que cada número de 10 a 99 é composto de dois dígitos, um é um número na casa das "unidades" e o outro número na casa das "dezenas". Mostre que o número "4" representa "quatro" quando está na casa das "unidades", mas serve como um prefixo para o número "40" quando está na casa das "dezenas".
- Ilustre o lugar das "unidades". Instrua a classe a nomear todos os números que têm o dígito "3" na casa dos "uns": 3, 13, 23, 33, 43, 53, 63, 73, 83, 93.
- Explique sobre o lugar das "dezenas". Instrua os alunos a designar todos os números que têm um "2" no lugar de "dezenas": 20, 21, 22, 23, 24, 25, 26, 27, 28, 29. Explique que o "3" em "23" é empilhados em cima de "20" marcado com o número "2". Ensine seus filhos a ler o lugar "dezenas" como um gatilho para o aprendizado.

Etapa 4. Experimente outras ferramentas de ensino visual
Você pode organizar objetos físicos ou desenhá-los no quadro. Você pode explicar o valor posicional usando incrementos de valor monetário, que os alunos podem já ter estudado, para relacioná-los a valores numéricos em escala. Para uma atividade divertida e interativa, tente usar os próprios alunos como um valor de "grupo".
A memória humana é dominada por coisas visuais, então o conceito de valor de lugar ainda é abstrato até que você possa torná-lo visual. Enquanto isso, os próprios símbolos numéricos ainda podem ser abstratos para crianças! Procure maneiras de enquadrar a contagem de grupos e as atividades de valor de posição de forma que sejam simples, tangíveis e intuitivas
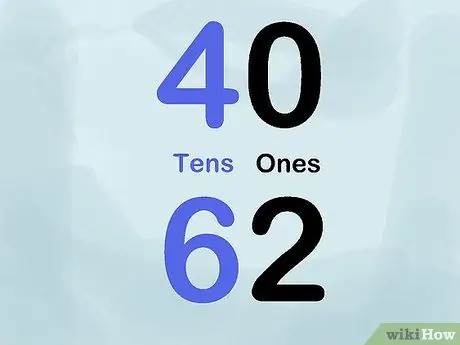
Etapa 5. Use cores
Tente usar giz ou marcadores de cores diferentes para demonstrar o valor posicional. Por exemplo, escreva vários números com um marcador preto para a casa "uns" e um marcador azul para a casa "dezenas". Assim, você escreveria 40 com o número "4" em azul e o número "0" em preto. Repita este truque para um grande número de números para mostrar a aplicação do valor posicional no tabuleiro.
Parte 3 de 3: use exemplos interativos
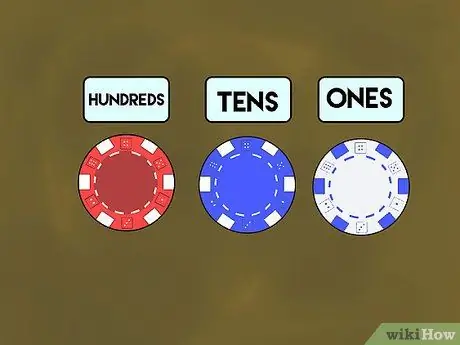
Etapa 1. Ensine com fichas de pôquer
Primeiro, distribua as fichas de pôquer para cada aluno. Diga a eles que as fichas brancas representam a casa dos "uns", as fichas azuis representam "dezenas" e as fichas vermelhas representam as "centenas". A seguir, mostre a seus alunos como fazer números usando valores posicionais na forma de fichas coloridas. Nomeie um número (digamos 7) e coloque a ficha branca à direita de sua mesa.
- Nomeie outro número - por exemplo, 30. Coloque três fichas azuis que representam 3 (na casa das "dezenas") e zero fichas brancas para representar 0 (na casa das "unidades").
- Você não precisa usar fichas de pôquer. Você pode usar qualquer objeto para representar os três valores básicos de "posição", desde que cada grupo (cor da ficha etc.) seja padrão, homogêneo e facilmente reconhecível.

Etapa 2. Instrua os alunos a trocarem peças entre si
Este método pode ilustrar os valores de casas baixos que constituem os valores de casas mais altos. Depois que os alunos tiverem demonstrado um bom entendimento do valor posicional, ensine sua classe como trocar fichas "uns" brancas por fichas "dez" azuis e, em seguida, troque fichas "dez" por "centenas". Pergunte aos alunos: "Quantas fichas azuis eu ganho trocando 16 fichas brancas? Se eu trocar três fichas azuis, quantas fichas brancas eu ganho?"

Etapa 3. Mostre como fazer adição e subtração com fichas de pôquer
Este conceito só pode ser ensinado depois que os alunos tiverem dominado a troca de fichas de pôquer. É útil começar escrevendo um exemplo.
- Para o problema de adição básica, instrua os alunos a estabelecerem três blue chips (dezenas) e seis white chips (uns). Pergunte aos alunos sobre os números formados com as fichas. (A resposta é 36!)
- Continue trabalhando no mesmo número. Peça aos alunos que adicionem cinco fichas brancas ao número 36. Pergunte a eles sobre o número atual. (A resposta é 41!) Em seguida, pegue uma ficha azul e pergunte o número atual. (A resposta é 31!)






